29 Time-dependence: sudden and adiabatic approximations
All of the approximation methods we’ve studied so far are static; they are methods for finding energy eigenvalues and eigenstates. While this can be used to get some information about time dependence, there is a lot to gain by considering more explicit methods for approximation that build in time evolution as well. We also, as of yet, have very few tools to handle the situation where the Hamiltonian itself has explicit time dependence.
We’ll begin with the sudden and adiabatic approximations, in which the nature of the time-dependence itself (very fast or very slow) allows us to make useful approximations. Then we’ll turn to a more general discussion of time-dependent perturbation theory.
29.1 Sudden approximation
We begin with the simpler approximation, which is the sudden approximation. The idea is simply that there is a sudden change to our Hamiltonian, which means that at some time t_S, the Hamiltonian suddenly changes from one form to another. Labelling the initial Hamiltonian as \hat{H}_0 and the new Hamiltonian as \hat{H}_1, then, \hat{H} = \begin{cases} \hat{H}_0,& t < t_S; \\ \hat{H}_1,& t \geq t_S. \end{cases}
This approximation is the simplest version of time dependence we can consider, since aside from the sudden jump at t_S, at all times we have a time-independent Hamiltonian governing the time evolution of our system. The experimental situation described by such a Hamiltonian is also sometimes known as a quantum quench, since it represents a sudden and instant change to the system (like suddenly putting a hot iron into water.)
In the approximation we have written a truly instant (step-function) time dependence, but in the real world nothing is truly instantaneous. The actual crossover from \hat{H}_0 to \hat{H}_1 will involve some transition time \tau_S over which the Hamiltonian is changing. The statement of the sudden approximation is that \tau_S is sufficiently short that any time evolution of the initial state \ket{\psi(t)} to \ket{\psi(t+\tau_S)} is negligible. Let’s be more concrete: the “real” Hamiltonian we’re imagining is \hat{H} = \begin{cases} \hat{H}_0,& t < t_S ; \\ \hat{H}_{T}(t), & t_S \leq t \leq t_S + \tau_S; \\ \hat{H}_1,& t > t_S + \tau_S, \end{cases} with \hat{H}_T(t) interpolating between the two static Hamiltonians, i.e. \hat{H}_T(t_S) = \hat{H}_0 and \hat{H}_T(t_S + \tau_S) = \hat{H}_1.
We can always write a formal solution in the transition region as an integral over the time-dependent Hamiltonian, \ket{\psi(t_S + \tau_S)} = \exp \left( -\frac{i}{\hbar} \int_{t_S}^{t_S+\tau_S} dt' \hat{H}(t') \right) \ket{\psi(t_S)}. (This assumes that \hat{H}(t) and \hat{H}(t') commute with one another, or else things get even more complicated; we’ll ignore that complication since we’re doing a small-time expansion in which it won’t matter anyways.) In the limit of small \tau_S, the integral becomes (at first order in \tau_S) \int_{t_S}^{t_S+\tau_S} dt' \hat{H}(t') \approx \tau_S \hat{H}(t_S) = \tau_S \hat{H}_0 which leaves us with the evolution of the state as, expanding in energy eigenstates, \ket{\psi(t_S + \tau_S)} = \sum_n e^{-iE_n \tau_S/\hbar} \ket{E_n} = e^{-iE_0 \tau_S/\hbar} \sum_n e^{-i(E_n - E_0) \tau_S / \hbar} \ket{E_n}, pulling out an overall phase since we’re always free to do that, to emphasize that only the differences in energies are significant (we can always change where the value E=0 is located in our energies, equivalently.)
The point of these manipulations was to show that for the sudden approximation to be a good approximation, we must require that this state is approximately just \ket{\psi(t_s)}, meaning it will be valid so long as \tau_S \ll \frac{\hbar}{\Delta E} for all of the energy splittings \Delta E in our original Hamiltonian \hat{H}_0 (so, effectively, for whatever the largest splitting is, since that gives rise to the fastest time evolution.)
When this condition is satisfied, the content of the sudden approximation is simple: the state \ket{\psi(t_S)} simply stays the same as we switch the Hamiltonian, and then from t_S onwards is evolves according to the new Hamiltonian.
29.1.1 Example: quenching an oscillator
Although the approximation itself is very simple to state, the outcome of a quantum quench (i.e. a sudden change to the Hamiltonian) can often lead to interesting results. It provides a simple way to force a system away from an equilibrium point and thus cause more complicated time evolution. As a simple example, let’s consider the simple harmonic oscillator \hat{H}_0 = \frac{\hat{p}^2}{2m} + \frac{1}{2} m \omega_0^2 \hat{x}^2 as our initial Hamiltonian, and then suppose that we simply change the frequency suddenly, so \hat{H}_1 = \frac{\hat{p}^2}{2m} + \frac{1}{2} m\omega_1^2 \hat{x}^2.
As usual, to answer any questions about these systems it’s going to be most useful to work with the ladder operators; we now have two sets of ladder operators, built from the same \hat{x} and \hat{p} but with different frequencies. Let’s remind ourselves of the definitions: \hat{a}_0 = \sqrt{\frac{m\omega_0}{2\hbar}} \left( \hat{x} + \frac{i\hat{p}}{m\omega_0} \right), \hat{a}_1 = \sqrt{\frac{m\omega_1}{2\hbar}} \left( \hat{x} + \frac{i\hat{p}}{m\omega_1} \right). We can rewrite both \hat{x} and \hat{p} in terms of either set of ladder operators. Doing so for \hat{a}_0 and its conjugate and then plugging back in, we find the result \hat{a}_1 = \sqrt{\frac{m\omega_1}{2\hbar}} \left( \sqrt{\frac{\hbar}{2m\omega_0}} (\hat{a}_0^\dagger + \hat{a}_0) + \frac{i}{m\omega_1} \left[ i \sqrt{\frac{\hbar m \omega_0}{2}} (\hat{a}_0^\dagger - \hat{a}_0) \right] \right) \\ = \frac{1}{2} \left( \sqrt{\frac{\omega_1}{\omega_0}} - \sqrt{\frac{\omega_0}{\omega_1}} \right) \hat{a}_0^\dagger + \frac{1}{2} \left( \sqrt{\frac{\omega_1}{\omega_0}} + \sqrt{\frac{\omega_0}{\omega_1}} \right) \hat{a}_0. To go backwards, (i.e. for \hat{a}_0 in terms of \hat{a}_1), we can just swap the labels 0 and 1.
Now suitably equipped, we’re ready to ask what happens to the system when we quench. One of the simplest possibilities is actually when the initial state is a coherent state of \hat{H}_0, \ket{\psi(0)} = e^{-|\alpha|^2/2} e^{\alpha \hat{a}_0^\dagger} \ket{0_0}. After the quench, the correct ladder operators are \hat{a}_1, not \hat{a}_0. But by construction, \ket{\psi(0)} is still an eigenstate of \hat{a}_0, a ladder operator with the “wrong frequency”. You may recall that we’ve encountered this situation before (back in Section 6.4.1): this is precisely a squeezed state! We can now see that a simple way to prepare such a state, which will be a minimum-uncertainty wave packet but with uncertainty set by frequency \omega_0 even as it evolves under oscillator \omega_1, is through a quantum quench.
As a simpler example to work with, let’s suppose that we begin in the ground state \ket{0_0} of \hat{H}_0. After the quench, it will evolve in time according to the new Hamiltonian \hat{H}_1. We know that \hat{a}_0 \ket{0_0} = 0. Substituting the new ladder operators in, (\omega_0 - \omega_1) \hat{a}_1^\dagger \ket{0_0} = (\omega_0 + \omega_1) \hat{a}_1 \ket{0_0}. Now we expand as a power series in the new basis, \ket{0_0} = \sum_{m=0}^\infty c_m \ket{m_1} \\ \Rightarrow (\omega_0 - \omega_1) \sum_{m=0}^\infty c_m \hat{a}_1^\dagger \ket{m_1} = (\omega_0 + \omega_1) \sum_{m=0}^\infty c_m \hat{a}_1 \ket{m_1} \\ (\omega_0 - \omega_1) \sum_{m=0}^\infty c_m \sqrt{m+1} \ket{(m+1)_1} = (\omega_0 + \omega_1) \sum_{m=0}^\infty c_m \sqrt{m} \ket{(m-1)_1} Now we can match term-by-term. Let’s do the first couple explicitly just to get the idea: 0 = (\omega_0 + \omega_1) c_1 \ket{0_1} \\ (\omega_0 - \omega_1) c_0 \ket{1_1} = (\omega_0 + \omega_1) \sqrt{2} c_2 \ket{1_1} \\ (\omega_0 - \omega_1) \sqrt{2} c_1 \ket{2_1} = (\omega_0 + \omega_1) \sqrt{3} c_3 \ket{2_1} and if we shift the sums to find a general recurrence relation, we see that (\omega_0 - \omega_1) c_{m-1} \sqrt{m} \ket{m_1} = (\omega_0 + \omega_1) c_{m+1} \sqrt{m+1} \ket{m_1} \\ \Rightarrow c_{m+2} = \frac{\omega_0 - \omega_1}{\omega_0 + \omega_1} \sqrt{\frac{m+1}{m+2}} c_{m}. This recurrence relation is actually quite simple: solution in Mathematica yields the result c_{2n} = c_0 \left( \frac{\omega_0 - \omega_1}{\omega_0 + \omega_1} \right)^n \sqrt{\frac{\Gamma(n+\tfrac{1}{2})}{\sqrt{\pi} n!}} for the even coefficients, while all of the coefficients for odd states are zero since c_1 = 0 (this is due to parity symmetry, which is fully preserved during the quench.) At very large n, the factorial dependence between the gamma function and the denominator cancel, and the second factor goes asymptotically to \sqrt{\frac{\Gamma(n+\tfrac{1}{2})}{\sqrt{\pi} n!}} \rightarrow \frac{1}{(\pi n)^{1/4}}. Since we also know that \omega_0 - \omega_1 < \omega_0 + \omega_1, we see that the state produced by the quench is a combination of all even states of the new oscillator \hat{H}_1, but with coefficients dying off with increasing n; the closer the new frequency \omega_1 is to the old one \omega_0, the more rapidly the coefficients die off (so we stay closer to the ground state of the new system if the change in frequency is smaller.)
Either before or after the quench, total energy is conserved, but we can see what happened to the energy during the quench. Doing the sums to find c_0 and then the average energy is all tractable, and the result is \Delta E = \frac{\hbar (\omega_0^2 + \omega_1^2)}{4\omega_0} - \frac{\hbar \omega_0}{2} = \frac{\hbar (\omega_1^2 - \omega_0^2)}{4\omega_0}. We can see that if the frequency increases after quenching \omega_1 > \omega_0, then the energy of the system increases, and vice-versa.
We could go on to look at time evolution of expectation values, although some of the simpler ones are trivial, for example \left\langle \hat{x}(t) \right\rangle = 0 through the quench because parity is conserved. But what we find won’t be too exciting: after the quench the system evolves according to \hat{H}_1, so everything will oscillate according to the new frequency \omega_1. If we track the full time evolution, we see that something discontinuous and dramatic happens at t=t_S when we quench, unsurprisingly.
29.2 Adiabatic approximation
Taking the opposite limit from the sudden approximation, we can look at the case where the time evolution of the Hamiltonian is extremely slow (i.e. adiabatic) rather than extremely fast. Timescales in quantum systems tend to be very fast compared to the macroscopic timescales that we live at, so the adiabatic approximation naturally shows up in more places than the sudden approximation.
For studying the adiabatic approximation, a useful starting point is to define instantaneous energy eigenstates, which come from diagonalizing a time-dependent Hamiltonian at a specific time t: \hat{H}(t) \ket{E_n(t)} = E_n(t) \ket{E_n(t)}. We can always find these states, but it’s very important to realize that their time evolution comes strictly from how the Hamiltonian changes in time, which means they are missing something. One way to see the problem is to recall that there is always an ambiguity in how we define the energy eigenstates: if \ket{E_n} is an energy eigenstate, then so is e^{i\phi} \ket{E_n}. If our basis is time-independent, then such phases have no physical effect. But if we allow ourselves to change our basis at every time t, then we can introduce an arbitrary phase each time we do so, meaning that \ket{E_n(t)} and e^{i\phi(t)} \ket{E_n(t)} are both perfectly good instantaneous energy eigenstates (you can see they both satisfy the equation above.) But they evolve differently in time; if one of them satisfies the Schrödinger equation, the other generally will not!
To resolve this ambiguity, let’s be more careful about how we track our time evolution. Rather than just treating \hat{H}(t) as having arbitrary time dependence, let’s take a parametric approach: we assume there are some parameters \theta^i, take the Hamiltonian to be a function of those parameters (\hat{H} \rightarrow \hat{H}(\theta^i)), and then introduce time dependence by varying the parameters in time (\theta^i \rightarrow \theta^i(t)). The index i allows us to have an arbitrary number of parameters, arranged in a “vector” in some fictitious space. Below I will suppress the index within \hat{H}(\theta) and E_n(\theta) just to make the following derivation cleaner, but there is no symmetry that requires us to have only fully contracted indices in our Hamiltonian, so in general \hat{H}(\theta^i) is the more general thing to write.
As a result of parametrizing the Hamiltonian, the energy eigenvalues and eigenstates also take on parametric dependence, \hat{H}(\theta) \ket{E_n(\theta)} = E_n(\theta) \ket{E_n(\theta)}. This is the same sort of parametric dependence that appeared for perturbation theory, taking \hat{H} = \hat{H}_0 + \lambda \hat{V}.
Critically, this deals with the ambiguity: once we specify the function \theta^i(t), it encodes the explicit time dependence of the instantaneous energy eigenstate \ket{E_n(\theta(t))}; no more ambiguous phases will show up. A smooth function \theta^i(t) ensures the phase will evolve smoothly in time. (There is a further ambiguity hiding here which is very important physically, but we’ll get to that below.)
Let’s consider the time evolution of a general quantum state \ket{\psi(t)} which does solve the Schrödinger equation. We can expand such a state in time-dependent coefficients times the (also time-dependent) instantaneous eigenstates, \ket{\psi(t)} = \sum_n c_n(t) \ket{E_n(\theta(t))}. Just to be clear, we are still working in Schrödinger picture here: the time-dependence of the energy eigenstates is explicitly from the Hamiltonian. We could, in principle, always expand in a time-independent basis (like \ket{\uparrow} and \ket{\downarrow} for a two-state system.) Rather than solve this directly, it will be a bit clearer to adopt a form in which we pull out the “expected” time dependence due to the energy eigenvalues, \ket{\psi(t)} = \sum_n a_n(t) e^{-i\xi_n(t)} \ket{E_n(\theta(t))}, where \xi_n(t) \equiv \frac{1}{\hbar} \int_0^t dt' E_n(t'). If we go back to a time-independent Hamiltonian, then e^{-i\xi_n(t)} is the usual energy phase and a_n(t) becomes time-independent, giving back the expected result in that case. Now let’s plug in to the time-dependent Schrödinger equation. We find: i \hbar \frac{\partial}{\partial t} \ket{\psi(t)} = \hat{H} \ket{\psi(t)} \\ i \hbar \sum_n \left[ \frac{da_n}{dt} - ia_n(t) \frac{d\xi_n(t)}{dt} + a_n(t) \frac{d\theta^i}{dt} \frac{\partial}{\partial \theta^i} \right] e^{-i\xi_n(t)} \ket{E_n(\theta(t))} \\ = \sum_n E_n(\theta(t)) a_n(t) e^{-i\xi_n(t)} \ket{E_n(\theta(t))}. The derivative d\xi_n/dt cancels the integration and simply gives back E_n(t)/\hbar, so that the middle term simply cancels against the right-hand side (as it should, since this was the point of including this “expected” time-dependence in our expansion.) Note also that the parameter index i now shows up and is implicitly summed over (Einstein summation convention.) Thus, the equation simplifies to \sum_n e^{-i\xi_n(t)} \left[ \frac{da_n}{dt} \ket{E_n(\theta(t))} + a_n(t) \frac{d\theta^i}{dt} \frac{\partial}{\partial \theta^i} \ket{E_n(\theta(t))} \right] = 0. Let’s try to understand what the mysterious-looking derivative of the basis ket with respect to \theta^i signifies. If we take a \theta derivative of the eigenvalue equation, we have \frac{\partial \hat{H}}{\partial \theta^i} \ket{E_n(\theta)} + \hat{H} \frac{\partial}{\partial \theta^i} \ket{E_n(\theta)} = \frac{\partial E_n}{\partial \theta^i} \ket{E_n(\theta)} + E_n \frac{\partial}{\partial \theta^i} \ket{E_n(\theta)}
Now we can dot in another energy eigenstate to simplify; at any time t the basis of eigenstates is still orthonormal, so choosing \ket{E_m(t)} distinct from \ket{E_n(t)}, (E_n - E_m) \bra{E_m(\theta)} \frac{\partial}{\partial \theta^i} \ket{E_n(\theta)} = \bra{E_m(\theta)} \frac{\partial \hat{H}}{\partial \theta^i} \ket{E_n(\theta)}. This lets us go back to our time-dependent Schrödinger equation and also dot in \bra{E_m(\theta(t))} on the left. Suppressing the \theta(t) to keep things shorter, \frac{da_m}{dt} e^{-i\xi_m(t)} + e^{-i\xi_m(t)} a_m(t) \frac{d\theta^i}{dt} \bra{E_m} \frac{\partial}{\partial \theta^i} \ket{E_m} = -\sum_{n \neq m} a_n(t) e^{-i\xi_n(t)} \bra{E_m} \frac{\partial}{\partial \theta^i} \ket{E_n} \frac{d\theta^i}{dt} \\ \frac{da_m}{dt} + a_m(t) \frac{d\theta^i}{dt} \bra{E_m} \frac{\partial}{\partial \theta^i} \ket{E_m} = -\sum_{n \neq m} a_n(t) e^{-i(\xi_n(t) - \xi_m(t))} \bra{E_m} \frac{\partial \hat{H}}{\partial \theta^i} \ket{E_n} \frac{d\theta^i/dt}{E_n - E_m}.
Now we finally come to the adiabatic approximation. The expression on the right-hand side is cumbersome, but it also has a small parameter in the explicit time variation d\theta^i / dt, relative to the energy splittings E_n - E_m. If our parameters vary slowly enough that we satisfy the condition \hbar \frac{d\theta^i}{dt} \ll E_n - E_m, then we can simply ignore the entire right-hand side and get the much simpler equation \frac{da_m}{dt} = +ia_m(t) \frac{d\theta^i}{dt} \mathcal{A}_i^{m}(\theta), defining the quantity known as the Berry connection (with an extra i pulled out for later convenience), \mathcal{A}_i^m(\theta) \equiv i \bra{E_m} \frac{\partial}{\partial \theta^i} \ket{E_m}. The beauty of this simplified differential equation for a_m is that all of the time dependence on the right-hand side is in the variation of the parameters d\theta^i/dt. That means that we can find the time-dependent solution for a_m simply by integration: a_m(t) = a_m(0) \exp \left( i \int_0^t dt' \mathcal{A}_i^m(\theta(t)) \frac{d\theta^i}{dt} \right) \equiv a_m(0) e^{i\gamma_n(\theta)}. The surprising thing that we should notice about the additional phase factor \gamma_n(\theta) is that, as my notation implies, it is sort of time-independent, even though it started as an integration over time: \gamma_m(\theta) = \int_0^t dt' \mathcal{A}_i^m(\theta(t)) \frac{d\theta^i}{dt} = \int_{\theta(0)}^{\theta(t)} d\theta^i \mathcal{A}_i^m(\theta) \\ = i \int_{\theta(0)}^{\theta(t)} d\vec{\theta} \cdot \bra{E_m} \vec{\nabla}_\theta \ket{E_m}, rewriting in vector notation to make it more evident that this is a line integral in the space defined by the parameter vector \vec{\theta}.
Restoring the full time dependence, c_n(t) = e^{i\gamma_n(\theta)} e^{-i\xi_n(t)} c_n(0). The first and most important fact to notice from this formula is that there is no cross-talk between different states \ket{E_n(t)}; the coefficients of state n at time t are determined by the coefficients at time zero. This gives us an important result:
Given a time-dependent Hamiltonian whose time evolution is encoded in a vector of parameters \theta^i, so that \hat{H}(t) = \hat{H}(\lambda(t)), if the time evolution satisfies the condition \hbar \frac{d\theta^i}{dt} \ll E_n - E_m for all parameters \theta^i and all energy eigenvalues E_m, E_n at all times, then for a quantum state \ket{\psi(t)} = \sum_n c_n(t) \ket{E_n(t)}, the energy-eigenstate coefficients evolve in time by picking up a pure phase, c_n(t) = e^{i\gamma_n(\theta)} e^{-i\xi_n(t)} c_n(0), with the dynamical phase given by \xi_n(t) \equiv \frac{1}{\hbar} \int_0^t dt' E_n(t') and the geometric phase equal to \gamma_n(t) \equiv i \int_{\theta(0)}^{\theta(t)} d\vec{\theta} \cdot \bra{E_m} \vec{\nabla}_\theta \ket{E_m}.
In particular, if the system begins in an energy eigenstate \ket{E_n}, it will remain in the same eigenstate \ket{E_n(\theta(t))} for all time.
Sometimes, the short version of the adiabatic theorem is simply given as the final statement, one which is physically intuitive: if we switch on a Hamiltonian and the time variation is slow enough, the system will respond by varying slowly and smoothly, and the composition of a state in terms of energy eigenstates will not change (as opposed to more sudden changes that can cause jumps between energy levels.)
In general, we can always realize a change which is adiabatic by slowing down d\theta^i/dt, but with one important exception: when E_n - E_m \rightarrow 0, known as a level crossing. Intuitively, if a level crossing happens, then at that point the two states are degenerate and can be mixed together arbitrarily, at which point we lose track of how much of the original state was in \ket{E_n} versus \ket{E_m}. The good news is that level crossings are very rare, since the degeneracy tends to indicate the presence of some symmetry that is being restored in the time evolution. If we don’t have such a symmetry to begin with, causing it to appear later on usually requires fine-tuning of the parameters.
29.3 Berry phase
The fact that energy eigenstates don’t mix together under adiabatic evolution is not that surprising. The larger surprise from the derivation above is the existence of the geometric phase, also known as Berry’s phase or simply a Berry phase. It depends on time only implicitly, in terms of the path taken through parameter space defined by \theta^i(t) (so the “geometry” on which it depends is the geometry of our fictitious parameter space, not the real geometry of space and time.) In some references, “Berry phase” will refer specifically to the case in which we follow a closed loop in parameter space where we return the system to where we started, so \theta(t) = \theta(0): \gamma_n = \oint_{\mathcal{C}} d\vec{\theta} \cdot \vec{\mathcal{A}}^n(\theta). where \mathcal{C} is a closed-loop path through parameter space. In this case the instantaneous energy eigenstates are the same before and after the evolution, \ket{E_n(t)} = \ket{E_n(0)}. But there is still a change to the quantum state, on top of the expected dynamical phase e^{-iE_n t/\hbar}; the system has some additional “memory” of how the parameters were changed, encoded in the Berry phase.
For the rest of this subsection, we’ll drop the index n and just focus on a single energy eigenstate, \ket{E_n(t)}. Restoring the parameter-space index, the Berry phase associated with evolution of this state is then \gamma = \oint_{\mathcal{C}} d\theta^i \mathcal{A}_i. This is, as we have already observed, completely independent of the specific parametrization \theta(t), only depending on the path through parameter space. But it is also invariant under certain other changes we can make. In particular, consider a modification of the Berry connection of the form \mathcal{A}_i' = \mathcal{A}_i + \frac{\partial \omega}{\partial \theta^i} for some function \omega(\theta). If we plug this back in to the formula for the Berry phase, \gamma' = \oint_{\mathcal{C}} d\theta^i \mathcal{A}_i' = \oint_{\mathcal{C}} d\theta^i \mathcal{A}_i + \oint_{\mathcal{C}} d\theta^i \frac{\partial \omega}{\partial \theta^i} \\ = \gamma + \oint_{\mathcal{C}} d\omega = \gamma with the d\omega integral vanishing since we come back to the same point, so the result is \omega(\theta) - \omega(\theta) = 0. So the Berry phase is invariant under such a change to the connection. This is good news, since a change of this form arises from a remaining ambiguity that we haven’t dealt with. Specifying the parameterization \theta(t) fixes the problem we raised above with the instantaneous energy eigenstates \ket{E_n(t)} picking up an arbitrary time-dependent phase e^{i\phi(t)}. But after the parameterization, we can still add an arbitrary phase to the eigenstates as long as it depends on \theta and not t directly: \ket{E_n(\theta)} \rightarrow e^{i\omega(\theta)} \ket{E_n(\theta)} gives an equivalent description of the physics. This rephasing causes a change to the Berry connection precisely as we wrote above, but doesn’t change the Berry phase. As we saw with gauge symmetry, this is an unphysical redundancy of our description, and so there cannot be physical consequences to the arbitrary changes given by \omega(\theta).
All of this should strongly remind you of our discussions of gauge symmetries; the Berry phase itself is very similar to the phase that appears in the Aharonov-Bohm effect. The key difference is that gauge symmetry is a symmetry involving paths through real space, while the Berry phase comes from paths through some parameter space. The mathematics used to describe these two different phenomena is very similar.
29.3.1 Example: neutron in a magnetic field
Let’s work through a simple example, looking at a single neutron in an external magnetic field, treating it as a two-state system. (Neutrons are spin-1/2 like electrons, but also electrically neutral, so we don’t have to worry about other ways they interact with the magnetic field in an experiment; for the purposes of the calculation we’re going to do here, they are treated the same.) We have already exhaustively looked at the time dependence of this system for various types of applied magnetic field, even certain time-dependent ones. But now, we’ll study what happens if the direction of the applied magnetic field is slowly rotated.
The Hamiltonian for this system takes the form \hat{H} = \frac{\hbar \omega}{2} \hat{\vec{\sigma}} \cdot \frac{\vec{B}}{|\vec{B}|} with \omega \equiv eg_n|\vec{B}|/(2m_nc). As we have already found (see Section 4.1.2), if we take the magnetic field direction described by \vec{B}/|\vec{B}| to be given by the spherical angles \theta and \phi, then the energy eigenstates are \ket{+} = \left( \begin{array}{c} \cos (\theta/2) \\ \sin (\theta/2) e^{i \phi} \end{array} \right), \\ \ket{-} = \left( \begin{array}{c} -\sin (\theta/2) \\ \cos (\theta/2) e^{i \phi} \end{array} \right), with corresponding energy eigenvalues E_\pm = \pm \hbar \omega/2.
So far this is all for a fixed magnetic field vector \vec{B}, but now we can take the magnetic field components (B_x, B_y, B_z) to be our parameter vector \theta^i. Allowing some slow time variation \vec{B}(t) then gives us the time-dependent Hamiltonian \hat{H}(t) we want, with the parameterization already built in. For this calculation, we’ll switch to spherical coordinates (|B|, \theta_B, \phi_B) in our parameter space as well. (It so happens that the way we have set things up, \theta_B and \phi_B are exactly the spherical angles describing the direction that the \vec{B}-field is pointing in real space as well, but don’t get confused; in general the parameter space is entirely separate!)
First of all, by the adiabatic theorem we’re guaranteed that if we begin in one of the energy eigenstates, we will stay in that state for all time. Let’s take the state \ket{+} to be our initial state; the results will of course be basically the same if we use \ket{-} instead.
One of the features we discussed previously regarding the two-state system solutions is that the energy eigenstates can “switch places” depending on exactly what the Hamiltonian looks like - in the solution of Section 4.3, this happens depending on the phase of the off-diagonal element \delta. Indeed, we can just plug in some specific choices of spherical angles above to see this effect: if we take \theta = \pi/2 and \phi = 0, then \ket{+} \rightarrow \frac{1}{\sqrt{2}} \left( \begin{array}{c} 1 \\ 1 \end{array} \right) \\ \ket{-} \rightarrow \frac{1}{\sqrt{2}} \left( \begin{array}{c} -1 \\ 1 \end{array} \right) \\ but if we change the phase to \phi = \pi, then \ket{+} \rightarrow \frac{1}{\sqrt{2}} \left( \begin{array}{c} 1 \\ -1 \end{array} \right) \\ \ket{-} \rightarrow \frac{1}{\sqrt{2}} \left( \begin{array}{c} 1 \\ 1 \end{array} \right) \\ So changing the phase causes our two eigenstates to switch places: \ket{S_{x,+}} is the negative energy state \ket{+} at \phi = \pi/2, but it’s the positive energy state \ket{-} if \phi = 0.
The key point to realize here is that although the two energy eigenstates “switch places” in terms of the \hat{S}_z basis (or any other basis) as we vary the angle, what the adiabatic theorem guarantees is that they vary smoothly as they swap. In other words, if we start in \ket{+} = \ket{S_{x,-}} at \phi = 0 and then slowly change the Hamiltonian until \phi = \pi, we will stay in \ket{+} - the energy won’t change - but the state vector will switch to \ket{S_{x,+}}.
Given a path \mathcal{C} through parameter space, then, the resulting Berry phase will be \gamma = \oint_{\mathcal{C}} d\theta^i \mathcal{A}_i = \oint_{\mathcal{C}} (|B| d\theta_B \mathcal{A}_\theta + |B| \sin \theta_B d\phi_B \mathcal{A}_\phi), substituting in the spherical line element in parameter space - it may be a fictitious space, but we still have to keep track of geometric factors when we change coordinates!
Now we need the value of the Berry connection, which is easily computed since we have the instantaneous eigenstates. However, we do have to be careful about geometric factors again: the general definition of the Berry connection is \vec{\mathcal{A}}^n = i \bra{n(\theta)} \vec{\nabla}_\theta \ket{n(\theta)} which means that in our spherical coordinates, \mathcal{A}_\theta^+ = \frac{i}{|B|} \bra{+} \frac{\partial}{\partial \theta_B} \ket{+} = 0, \\ \mathcal{A}_\phi^+ = \frac{i}{|B| \sin \theta_B} \bra{+} \frac{\partial}{\partial \phi_B} \ket{+} = -\frac{\sin^2 (\tfrac{\theta_B}{2})}{|B| \sin \theta_B}. \\ This is everything we need to calculate the Berry phase for a given curve \mathcal{C}. A simple and interesting class of curves \mathcal{C}_\theta are defined by holding \theta_B fixed at some angle, and then varying \phi in a complete circle from 0 to 2\pi. The resulting Berry phase is \gamma_\theta^+ = |B| \int_0^{2\pi} d\phi_B \sin(\theta_B) \left(-\frac{\sin^2 (\tfrac{\theta_B}{2} )}{|B| \sin (\theta_B)}\right) \\ = -2\pi \sin^2(\theta_B/2) = -\frac{\Omega_B}{2}, where \Omega_B is precisely the solid angle subtended by the part of the sphere within the curve \mathcal{C}_\theta. (For example, if we take an equatorial path \theta_B = \pi/2, the solid angle subtended is 2\pi - half of the entire sphere - and the resulting Berry phase is -\pi.) If we repeat the calculation for the other energy eigenstate, we find the result \gamma_\theta^- = -2\pi \cos^2(\theta_B/2) = -2\pi (1 - \sin^2(\theta_B/2)) = - \frac{(4\pi - \Omega_B)}{2}.
What is the physical consequence of this phase? If we just have a single initial state \ket{\psi} and track its evolution, the Berry phase is unobservable since it amounts to an overall global phase. To observe its presence, we need to compare to a second state that doesn’t have the phase. Let’s consider a Mach-Zehnder interferometer as the setup:
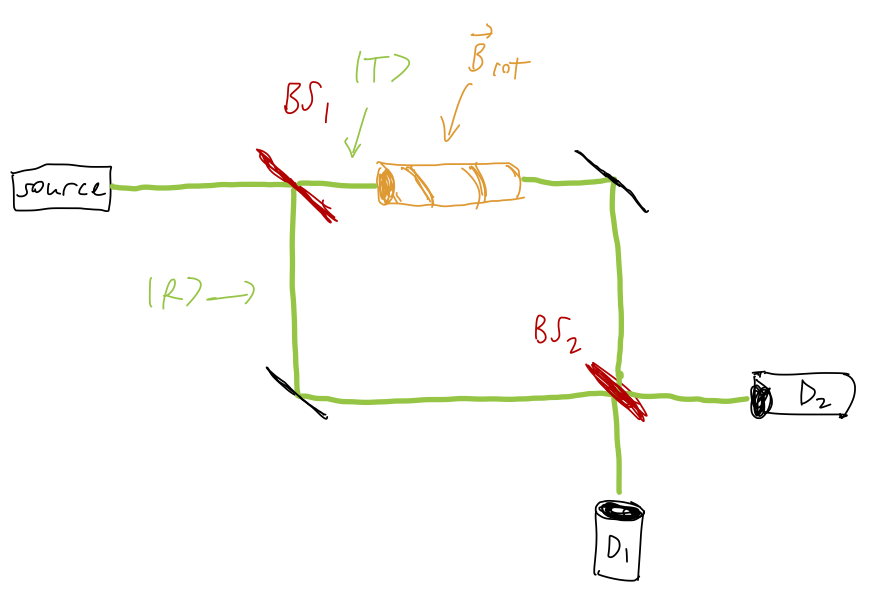
Our input beam encounters a beam splitter, which has the effect of splitting it into two beams, reflected R and transmitted T. Since there are two paths along which our particles can propagate from input to output, we can effectively describe this experiment in terms of a two-state Hilbert space consisting of \ket{R} and \ket{T}. The beam splitter itself can be described as a unitary operation that maps the two input states \ket{I_1}, \ket{I_2} to the output states \ket{O_1}, \ket{O_2} as \hat{U}_{BS} = \frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1 & i \\ i & 1 \end{array} \right). Now, suppose we have an input beam of electrons prepared in the state \ket{-}. After the first beam splitter, the state of the system becomes \ket{\psi_{MZ,{\rm in}}} = \frac{1}{\sqrt{2}} (\ket{R} + i\ket{T}) \otimes \ket{-} where we have a direct-product state encoding the spatial state times the spin state. Next, as pictured, we subject the transmitted arm of the interferometer to a time-varying rotating magnetic field of magnitude |B_{\rm rot}| in the xy plane, while the other arm remains in a constant magnetic field; we set things up in such a way that |\vec{B}| is held fixed everywhere. In propagating from the first to second beam splitter, then, each arm will pick up a dynamical phase, \xi_R(t) = \frac{1}{\hbar} \int_0^L dt' E_n(t') = -\frac{\omega t}{2} where L is the length of the path of travel and \xi_T = \xi_R since the magnetic field strength is fixed. The transmitted state only will pick up a geometric phase as well, according to the solid angle subtended by the magnetic field rotation. Thus, at the input to the second beam splitter, we have \ket{\psi_{MZ,{\rm out}}} = \frac{1}{\sqrt{2}} \left( e^{-i\omega t/2} \ket{R} \otimes \ket{-} + ie^{-i\omega t/2} e^{-i\Omega_B t/2} \ket{T} \otimes \ket{-} \right) Applying the second beam splitter as another unitary operator (on the spatial components) relates this state to the output states at detector 1 or detector 2, \ket{\psi_f} = \frac{1}{2} e^{-i\omega t/2} \left[ (1-e^{-i\Omega_B t/2}) \ket{D_1} + i(1+e^{-i\Omega_B t/2}) \ket{D_2} \right]. Now if we read out, say, detector 1, we find the neutron with probability p(D_1) = |\left\langle D_1 | \psi_f \right\rangle|^2 = \frac{1}{4} |1-e^{-i\Omega_B t/2}|^2 = \frac{1}{2} - \frac{1}{2} \cos \left( \frac{\Omega_B t}{2} \right).
Although plausible, realistic experimental measurements of the Berry phase using neutrons (see e.g. this paper by Bitter and Dubbers) use different setups that are a bit more complicated to describe. There have also been Berry phase measurements done using an interferometer setup like this, but generally using photons and not neutrons.
In the limit that we take the solid angle to be the entire sphere, \Omega_B \rightarrow 4\pi, we find that the Berry phase is -2\pi. This might not seem remarkable, but it is a manifestation of a powerful and general result, which is that if we integrate over any curve that defines a closed surface (in this example, the entire sphere), the resulting Berry phase is always an integer multiple of 2\pi, \gamma_{\rm closed} = 2\pi C, where the integer C is known as the Chern number. There are deep connections to the mathematics of electromagnetism and gauge theory here, and this result can be understood and proved in terms of fictitious ``monopole charges’’ and Gauss’s law, but in the parameter space and not in real space! If you’d like to read more about this I recommend (as I often do here) the discussion in David Tong’s advanced quantum lecture notes.
There are practical and interesting effects of the Berry phase in certain quantum systems, notably when studying band structure in crystals; it can also be used as a way to understand the quantum Hall effect. We won’t dig into either of these topics here, but just to motivate that the Berry phase is more than just a curiosity.
29.4 Time reversal
Although it isn’t an approximation method in and of itself, time reversal symmetry can be a powerful tool in constraining what can happen when a system evolves in time, so it’s worth considering here. Time reversal is similar to parity, in that it’s just an inversion of one of our coordinates, mapping t \rightarrow -t. But because time plays a special role in quantum mechanics (with time evolution being included in the postulates explicitly), the consequences are quite different.
As a warm-up, let’s remind ourselves that time reversal is a good symmetry of (conservative) classical mechanics. Given a classical Hamiltonian of the form H = p^2/(2m) + V(x), the equation of motion is m \ddot{x} = -\frac{\partial V}{\partial x}. Because only the second derivative appears, inverting t \rightarrow -t leaves this equation invariant. Another way to state this is that if x(t) solves the equations of motion, so does x(-t). This means that if we record a movie of a classical system evolving in time, and then play the movie backwards, either trajectory that we observe will be consistent with Newton’s laws.
To transfer this idea into quantum mechanics, following our earlier treatment of parity, we have to define an operator that will take t \rightarrow -t. However, our first problem is that the Schrodinger equation will not be invariant under just reversing time, since it depends on the first time derivative of the wavefunction and not the second: i\hbar \frac{\partial \psi}{\partial t} = \hat{H} \psi. But now we notice the i in front of the time derivative; if we both reverse time and complex conjugate the equation, then the result is unchanged. In other words, \psi^\star(x,-t) and \psi(x,t) obey the same equation of motion. This suggests that the time-reversal operator has to return the conjugate of the wavefunction, in addition to flipping the sign of time.
We can proceed by trying to expand \ket{\psi(t)} out and consider what the time-reversal operator has to look like to give this behavior, but because \psi^\star(x,t) is most conveniently thought of as a bra \bra{\psi(t)}, things will quickly get confusing. Instead, as with parity, it’s better to start in the operator picture and describe how it acts there. As a reminder, parity acts on some familiar vectors as follows: \hat{P}^{-1} \hat{\vec{x}} \hat{P} = -\hat{\vec{x}},\ \ \hat{P}^{-1} \hat{\vec{p}} \hat{P} = -\hat{\vec{p}},\ \ \hat{P}^{-1} \hat{\vec{L}} \hat{P} = -\hat{\vec{L}}. If we call the time reversal operator \hat{\Theta}, then we have the following action for the same vectors: \hat{\Theta}^{-1} \hat{\vec{x}} \hat{\Theta} = +\hat{\vec{x}},\ \ \hat{\Theta}^{-1} \hat{\vec{p}} \hat{\Theta} = -\hat{\vec{p}},\ \ \hat{\Theta}^{-1} \hat{\vec{L}} \hat{\Theta} = -\hat{\vec{L}}. Briefly, the position operator doesn’t depend on time, so \Theta doesn’t affect it; but both linear and angular momentum have single time derivatives in their definitions, so they are reversed by \Theta.
Now, there is an important relation between position and momentum; as we discussed in Section 10.4, identifying momentum as the generator of translation symmetry implies the canonical commutation relation [\hat{x}, \hat{p}] = i\hbar. Let’s try conjugating with \hat{\Theta} on this equation: \hat{\Theta}^{-1} (\hat{x} \hat{p} - \hat{p} \hat{x}) \hat{\Theta} = \hat{\Theta}^{-1} i\hbar \hat{\Theta} \\ \hat{\Theta}^{-1} (\hat{x} \hat{\Theta} \hat{\Theta}^{-1} \hat{p} - \hat{p} \hat{\Theta} \hat{\Theta}^{-1} \hat{x})\hat{\Theta} = \hat{\Theta}^{-1} i\hbar \hat{\Theta} \\ \hat{x} (-\hat{p}) - (-\hat{p}) \hat{x} = \hat{\Theta}^{-1} i\hbar \hat{\Theta} \\ -[\hat{x}, \hat{p}] = \hat{\Theta}^{-1} i\hbar \hat{\Theta}. Here I’ve deliberately not simplified the right-hand side yet. If we go too quickly and assume we can just collapse \hat{\Theta} \hat{\Theta} = \hat{1} on the right-hand side, then we end up with a contradiction; -i\hbar = i\hbar. What is going on?
Let’s be extra careful. Strictly speaking, what we have on the right-hand side is the operator \hat{\Theta}^{-1} times the operator i\hbar \hat{\Theta}. Our usual interpretation of multiplying an operator times a scalar relies on the property of linearity, that \hat{O}(c_\alpha \ket{\alpha} + c_\beta \ket{\beta}) = c_\alpha \hat{O} \ket{\alpha} + c_\beta \hat{O} \ket{\beta}. Linearity tells us that i\hbar \hat{\Theta} \ket{\alpha} should be the same thing as \hat{\Theta} (i\hbar \ket{\alpha}), which would let us cancel against its own inverse. So in order for a time reversal operator to exist, we can only conclude that it is not linear!
In fact, what we want to be true in order to preserve the canonical commutation relation is that i\hbar \hat{\Theta} \ket{\alpha} = -\hat{\Theta} (i\hbar \ket{\alpha}), which will fix the sign for us. This is the behavior of an anti-linear operator:
An anti-linear operator on a Hilbert space is an operator \hat{A}: \mathcal{H} \rightarrow \mathcal{H} which satisfies the condition \hat{A}(c_\alpha \ket{\alpha} + c_\beta \ket{\beta}) = c_\alpha^\star \hat{A} \ket{\alpha} + c_\beta^\star \hat{A} \ket{\beta}, i.e. it can still be distributed linearly over sums of kets, but it has the additional effect of complex conjugating their coefficients.
Anti-linear operators have some rather unintuitve properties, especially since we have become used to working in Dirac bra-ket notation - which, unfortunately, can be extremely misleading for some specific properties of anti-linear operators! Most importantly, for the linear operators we’ve encountered so far, the idea of “applying the operator to a bra” is well-defined through the inner product: \hat{O} \ket{\alpha} = \ket{\beta} \Rightarrow \bra{\alpha} \hat{O}^\dagger = \bra{\beta}, so if we’re handed a matrix element \bra{\alpha} \hat{O} \ket{\beta} we can always apply the operator to the left by conjugating it (we’ve done this frequently, for example when using SHO ladder operators.) In other words, (\bra{\alpha} \hat{O}) \ket{\beta} = \bra{\alpha} (\hat{O} \ket{\beta}).
This fails spectacularly for anti-linear operators! If we want to define \hat{A}^{\dagger}, or equivalently if we want to act on a bra to the left, we have to be extra careful and include some additional complex conjugation operations.
For these notes, I am not going to be so careful or general about anti-linear operators; see David Tong’s notes for a more careful treatment, or this paper if you really want all of the rigorous mathematical details. For time reversal, we can see the basic physical effects by always acting to the right on kets and not worrying about the adjoint (just keep in mind that you can’t manipulate \hat{\Theta} in all the same ways if matrix elements are involved!)
The anti-linearity of time reversal gives us exactly the behavior that we want in terms of how it interacts with the time evolution operator. If we start with a state \ket{\psi(0)}, its time evolution is given by the usual exponential of the Hamiltonian, \ket{\psi(t)} = e^{-i\hat{H} t/\hbar} \ket{\psi(0)}. If we act with \hat{\Theta}, the resulting state \hat{\Theta} \ket{\psi} = \ket{\psi_\Theta} should evolve backwards instead of forwards, meaning that: \ket{\psi_\Theta(-t)} = \hat{\Theta} \ket{\psi(t)} \\ e^{+i\hat{H} t/\hbar} \hat{\Theta} \ket{\psi(0)} = \hat{\Theta} e^{-i\hat{H} t/\hbar} \ket{\psi(0)} \\ \Rightarrow e^{i\hat{H} t/\hbar} \hat{\Theta} = \hat{\Theta} e^{-i\hat{H} t/\hbar}. This will be true thanks to the complex-conjugation that happens when we push \hat{\Theta} through the time evolution, so long as it commutes with the Hamiltonian, [\hat{H}, \hat{\Theta}] = 0.
So although the operator itself is strange, we recover the familiar statement that if \hat{\Theta} commutes with the Hamiltonian, then it is a dynamical symmetry of the system. But keep in mind that this is a very different kind of dynamical symmetry, in particular it doesn’t tell us that anything is conserved in time, it just relates forwards and backwards time evolution.
On top of being anti-linear, the time reversal operator \hat{\Theta} turns out to be anti-unitary, which means that it satisfies the property \bra{\chi} \hat{\Theta}^\dagger \hat{\Theta} \ket{\psi} = \left\langle \chi | \psi \right\rangle^\star = \left\langle \psi | \chi \right\rangle.
This is an example of the weirdness (in Dirac notation) that we have to deal with with anti-linear operators; it looks like the unitary condition \hat{U}^\dagger \hat{U} = \hat{1}, except we have to tack on a complex conjugation of the product.
Note that anti-unitary lets us connect back to the story we started with in terms of the Schrödinger equation, since using the fact that \hat{\Theta} \ket{\vec{x}} = \ket{\vec{x}} (since time reversal doesn’t affect the position vector at all), we see that \left\langle \vec{x} | \hat{\Theta} \psi \right\rangle = \left\langle \hat{\Theta} \vec{x} | \hat{\Theta} \psi \right\rangle = \left\langle \psi | \vec{x} \right\rangle = \psi^\star(x).
For time reversal, we should impose one more important physical constraint, which is that applying time reversal twice has to leave the physics of our system unchanged. This means that for any state \ket{\psi} in our Hilbert space, we must have \hat{\Theta}^2 \ket{\psi} = e^{i\alpha} \ket{\psi} where \alpha is a global phase, i.e. it is the same for all states in our space so that all physical observations will be unchanged. This ensures that time reversal squared is a symmetry in the sense of Wigner’s theorem. But now, we see that the following is true: e^{i\alpha} \hat{\Theta} \ket{\psi} = \hat{\Theta}^3 \ket{\psi} = \hat{\Theta} e^{i\alpha} \ket{\psi}, but at the same time by the anti-linearity of \hat{\Theta}, e^{i\alpha} \hat{\Theta} \ket{\psi} = \hat{\Theta} e^{-i\alpha} \ket{\psi}. So the only possible phases satisfy e^{i\alpha} = e^{-i\alpha}, which means \alpha = 0 or \alpha = \pi. In other words, the eigenvalues of \hat{\Theta}^2 are either \pm 1.
Once again, this should remind you of what we found previously with parity, except that it’s a bit stranger. For parity, we proved that the eigenvalues of \hat{P} itself were \pm 1, which means that applying it twice always gives the identity, \hat{P}^2 \ket{\psi} = \ket{\psi}. Here, we see that squaring time reversal (which should take us back to where we started) gives \pm 1 as the result. This still leaves the physics invariant since the -1 is a global phase, but it does actually have an important physical consequence.
29.4.1 Kramers degeneracy
With what we know about \hat{\Theta} so far, we have enough to say something interesting about how it acts on momentum eigenstates. The starting point is that for any angular momentum operator, conjugation by \hat{\Theta} should flip its sign, \hat{\Theta}^{-1} \hat{\vec{J}} \hat{\Theta} = -\hat{\vec{J}}. Now consider \hat{\Theta} acting on an eigenstate \ket{jm}, together with the z component: we have \hat{\Theta} \hat{J}_z \ket{jm} = \hbar m \hat{\Theta} \ket{jm} but also \hat{\Theta} \hat{J}_z \ket{jm} = -\hat{J}_z \hat{\Theta} \ket{jm} which means that \hat{\Theta} acting on \ket{jm} gives us back another \ket{jm} eigenstate, up to a constant. Specifically, \hat{J}_z (\hat{\Theta} \ket{jm}) = -\hbar m (\hat{\Theta} \ket{jm}) \Rightarrow \hat{\Theta} \ket{jm} = \theta_{jm} \ket{j,-m}. We can get more constraints on the phase using the other components of \hat{\vec{J}}. In particular, it’s easy to show that \hat{\Theta} \hat{J}_{\pm} = -\hat{J}_{\mp} \hat{\Theta}, which we can use to act with the lowering operator on the same state: \hat{\Theta} \hat{J}_- \ket{jm} = \hat{\Theta} \hbar \sqrt{(j+m)(j-m+1)} \ket{j,m-1} \\ = \hbar \sqrt{(j+m)(j-m+1)} \theta_{j,m-1} \ket{j, -m+1} \\ = \theta_{j,m-1} \hat{J}_+ \ket{j,-m}. But then commuting the operators, we also have \hat{\Theta} \hat{J}_- \ket{jm} = -\hat{J}_+ \hat{\Theta} \ket{jm} \\ = -\hat{J}_+ \theta_{jm} \ket{j,-m} so comparing, we see the relation \theta_{jm} = -\theta_{j,m-1}. Finally, we get one more condition from applying time reversal twice: \hat{\Theta}^2 \ket{jm} = \pm \ket{jm} \\ \hat{\Theta} \theta_{jm} \ket{j,-m} = \pm \ket{jm} \\ \theta^\star_{jm} \theta_{j,-m} \ket{jm} = \pm \ket{jm} so \theta^\star_{jm} \theta_{j,-m} = \pm 1. But from the alternating sign condition, \theta_{j,-m} = (-1)^{2m} \theta_{j,m}, which means that |\theta_{jm}|^2 = 1, i.e. \theta_{jm} has to be a pure phase. And if we put everything together, we can see that the combined solution to all of the conditions we found is \theta_{jm} = e^{i\pi m} = i^{2m}.
So we see something interesting here: if we consider \hat{\Theta}^2 specifically, we see that \hat{\Theta}^2 \ket{jm} = +\ket{jm} if j is an integer, but \hat{\Theta}^2 \ket{jm} = -\ket{jm} if j is half-integer. In other words, the eigenvalue of \hat{\Theta}^2 is +1 for bosons and -1 for fermions.
Now, suppose that we have a system which preserves time reversal, so that [\hat{H}, \hat{\Theta}] = 0, and consider the energy eigenstates \{\ket{E_n}\}. If time reversal commutes with the Hamiltonian, then \hat{\Theta} \ket{E_n} has the same energy as \ket{E_n}, which means they are equal up to a constant, \hat{\Theta} \ket{E_n} = c_n \ket{E_n}.
But then we apply \hat{\Theta} a second time: \hat{\Theta}^2 \ket{E_n} = \hat{\Theta} (c_n \ket{E_n}) \\ = c_n^\star \hat{\Theta} \ket{E_n} \\ = |c_n|^2 \ket{E_n}. If \hat{\Theta}^2 = +1, then c_n just has to be a pure phase and everything is fine. But if \hat{\Theta}^2 = -1 (i.e. if we are describing a fermion!), then this equation gives us a contradiction. The only way out is if \hat{\Theta} \ket{E_n} gives us a different state with the same energy - a degenerate pair. This is a powerful observation:
For any fermionic system for which time reversal is a dynamical symmetry, all energy eigenstates \ket{E_n} come in degenerate pairs.
For the familiar spin-1/2 system, the degenerate pair is just the two basis states \ket{+} and \ket{-} that we’re familiar with! Anytime they do not have the same energy, we know that we are working with a Hamiltonian that violates time-reversal symmetry. (For example, applying an external magnetic field \vec{B}, which is odd under time reversal - so that the system is not invariant unless we also flip the magnetic field backwards.)
This is a powerful constraint on a wide variety of systems, even systems that we can’t solve analytically, as long as they are time-reversal invariant. This includes arbitrarily complicated condensed matter systems, as long as they are overall fermionic (e.g. systems with an odd number of electrons.)
29.5 Density matrices and time dependence
Finally, we’ll finish our grab bag of time-dependence topics by coming back to density matrices. We have already showed that density matrices evolve in time according to the quantum Liouville-von Neumann equation, \frac{d\hat{\rho}}{dt} = \frac{1}{i\hbar} [\hat{H}, \hat{\rho}].
Under the sudden approximation, then, the statement is simply that if we have a rapid change in \hat{H} at time t_S the density matrix will remain unchanged, but from that time forward we switch out the Hamiltonian that appears in the time-evolution equation above. This follows simply from what we showed above, since \hat{\rho} = \sum_i \ket{\psi_i}\bra{\psi_i}, and each of the states \ket{\psi_i} doesn’t change as the Hamiltonian changes in the sudden approximation.
What about the adiabatic approximation? Our result from above was that if we write an arbitrary time-dependent state \ket{\psi(t)} in terms of energy eigenstates, then under adiabatic evolution it evolves as \ket{\psi(t)} = \sum_n e^{i\gamma_n(\theta)} e^{-i\xi_n(t)} c_n(0) \ket{E_n(t)}, picking up pure phases only. This immediately means that as long as we write it in the basis of instantaneous energy eigenstates \ket{E_n(t)}, the diagonal entries of the density matrix are \rho_{ii}(t) = \bra{E_i(t)} (\ket{\psi(t)} \bra{\psi(t)}) \ket{E_i(t)} = |c_i(0)|^2 = \rho_{ii}(0). In other words, under adiabatic evolution, diagonal elements of the density matrix in the instantaneous energy eigenbasis are constant. This broadens the previous statement of the adiabatic theorem, which is that “a system that begins in \ket{E_n} stays in \ket{E_n(t)}”; the density-matrix version of this statement is that if the system begins in a mixture of energy eigenstates, the mixture stays the same, i.e. the probability of measuring each energy E_n does not evolve in time.
On the other hand, the off-diagonal elements of the density matrix can change over time as they pick up different phases that don’t cancel; this is to be expected, since we know that e.g. Berry phases can be measured, so they have to appear in the density matrix. I won’t write out a detailed expression for this, but see this paper for detailed results on adiabatic evolution of density matrices.