3  The two-state system

One of the ways in which the Stern-Gerlach experiment is a really nice prototypical example of quantum mechanics is because the outcome is not only discrete (quantized), but it is as simple as possible: there are only two possible final states (two dots on the screen.) This makes the Stern-Gerlach experiment an example of a two-state system. A two-state system in quantum mechanics is simply a system for which only two states are needed to construct a complete basis, i.e. the Hilbert space is two-dimensional (in math notation, d(\mathcal{H}) = 2.)

Like the harmonic oscillator, the two-state system is ubiquitous in physics because it provides a good approximate description to a lot of realistic systems, and because we can solve it completely and exactly. A few other places you will encounter two-state quantum systems include:

Although I will make some references to Stern-Gerlach or other systems, since I want to emphasize how general the two-state system is, we’ll switch notation slightly: instead of \ket{\uparrow} and \ket{\downarrow}, which are natural labels for spin-up and spin-down, we’ll switch to just \ket{0} and \ket{1}. (We’ll do a lot of Stern-Gerlach in this chapter for which I’ll keep the arrows; the 0/1 qubit-oriented notation will persist into the next chapter.) From these two basis vectors, the most general state we can build is then \ket{\psi} = \alpha \ket{0} + \beta \ket{1}

which again, must be normalized, giving the restriction |\alpha|^2 + |\beta|^2 = 1. Applying normalization leaves three real numbers as free parameters. Let’s parameterize them in the following form: \ket{\psi} = e^{i\zeta} \left[\cos(\theta/2) \ket{0} + \sin(\theta/2) e^{i \phi} \ket{1} \right]. Because of the overall phase in front (which can flip the sign of the whole state), we can cover all possible values with \theta \in [0,\pi) and \phi \in [0, 2\pi). The number \zeta here is a global phase: we can simply absorb it without changing any of the physics. Basically, this is because only squared amplitudes are physical. Suppose we have a second arbitrary state \ket{\psi'}. Then the inner product of the two states is \left\langle \psi' | \psi \right\rangle = e^{i(\zeta - \zeta')} \left[ \cos(\theta'/2) \cos(\theta/2) + \sin(\theta'/2) \sin(\theta/2) e^{i(\phi-\phi')} \right].

But the state overlap itself is not observable - only the square of the overlap |\left\langle \psi' | \psi \right\rangle|^2 is, through Born’s rule (postulate 4.) The phases \phi and \phi' matter because they will survive in the square, but \zeta and \zeta' vanish from the probability no matter what.

WarningPhases in quantum mechanics

Don’t let the irrelevance of the global phase \zeta lull you into thinking that phases don’t matter in quantum mechanics. The relative phase of the two basis states within \ket{\psi}, \phi - \phi', is most certainly observable and will appear in the probabilities computed through Born’s rule.

Likewise, the state e^{-i\zeta} \ket{\psi} is not the same as \ket{\psi} in general! Again, from above, we can’t just take our basis state \ket{0} and rephase it - it will change the answer. This isn’t special to basis states: if I take two kets and add them together, \ket{\alpha} = \ket{\chi} + \ket{\psi}, rephasing either \ket{\chi} or \ket{\psi} (i.e. multiplying by e^{i\zeta}) will change \ket{\alpha} and result in observable changes in general.

So how do we tell which phases matter and which ones are irrelevant “global” phases? The key is to realize that the idea of a global phase is a statement about physical states, not about arbitrary kets. Any physical \ket{\psi} that we can perform measurements against is utterly indistinguishable from the state e^{i\zeta} \ket{\psi}. (Mathematically, the statement is that physical states exist in a projective Hilbert space; I won’t say more about the math but I wanted to give the term if you want to learn more.)

If in doubt, a good rule of thumb to remember is that you can always apply an arbitrary phase to your quantum state at the end of any given calculation, but it may not be safe to do so beforehand.

Based on the above, we only need two real numbers to fully describe an arbitrary physical state, \theta and \phi. As suggested by the use of angles, we can visualize this nicely as a point on the surface of a sphere (called the Bloch sphere after the physicist of the same name). The choice above corresponds to putting the states \ket{0} and \ket{1} at the north and south poles respectively:

Sketch of the Bloch sphere.

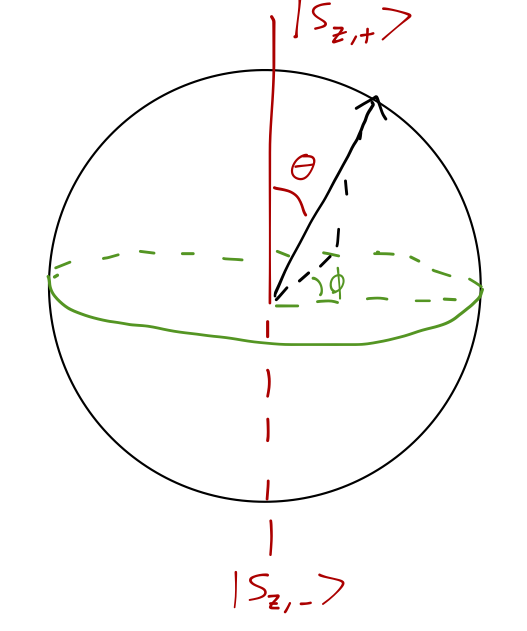
\ket{\psi} = \cos(\theta/2) \ket{0} + \sin(\theta/2) e^{i \phi} \ket{1}

(The choice of which is which is arbitrary, but \ket{0} as the north pole seems to be the common convention.) I should note in passing that only needing two real numbers is unique to the two-state system, i.e. for a three-state system, we would need four real parameters: three complex numbers, minus one normalization condition, minus one global phase.

3.1 Two-state observables; Pauli matrices

Now that we have a general description of quantum states, we need to think about observables. By postulate 2, any observable is Hermitian, which means we’re interested in all possible Hermitian two-by-two matrices. Here is the most general such matrix, written in terms of some real numbers w,x,y,z:

\hat{O} = \left( \begin{array}{cc} w+z & x-iy \\ x+iy & w-z \end{array}\right). Here we’ve just applied Hermiticity (\hat{O}^\dagger = \hat{O}), which tells us the diagonal entries are real (but can be different), while the off-diagonals must be complex conjugates of one another. I have written this in a suggestive form to allow me to split it into a sum over four “basis” matrices: \hat{O} = w \hat{1} + x \hat{\sigma}_x + y \hat{\sigma}_y + z \hat{\sigma}_z.

The operator \hat{1} is just the identity matrix, while the other three are a special set of matrices known as the Pauli matrices which we will encounter often:

ImportantPauli matrices

The Pauli matrices are defined as follows: \begin{aligned} \hat{\sigma}_x &\equiv \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) \\ \hat{\sigma}_y &\equiv \left( \begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right) \\ \hat{\sigma}_z &\equiv \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right). \end{aligned}

(Note that some references will label these as \hat{\sigma}_{1,2,3} instead.)

The Pauli matrices have some very useful properties which are straightforward to check:

  • They square to the identity: \hat{\sigma}_i^2 = \hat{1}.

  • They obey the commutation relations

\begin{aligned} [\hat{\sigma}_x, \hat{\sigma}_y] &= 2i \hat{\sigma}_z \\ [\hat{\sigma}_x, \hat{\sigma}_z] &= -2i \hat{\sigma}_y \\ [\hat{\sigma}_y, \hat{\sigma}_z] &= 2i \hat{\sigma}_x \\ \end{aligned}

or more compactly, [\hat{\sigma_i}, \hat{\sigma_j}] = 2i \epsilon_{ijk} \hat{\sigma_k} where \epsilon_{ijk} is the Levi-Civita symbol (see below if you’re not familiar with it.)

  • They obey the anti-commutation relation \{\hat{\sigma}_i, \hat{\sigma}_j\} = 2\delta_{ij} \hat{1}.

In case you aren’t familiar with it, the Levi-Civita symbol \epsilon_{ijk} is an object whose entries are either 1, -1, or 0, and it is totally antisymmetric under exchange of its indices. This tells you immediately what the whole tensor looks like, once we fix the convention that \epsilon_{xyz} = 1:

  • \epsilon_{ijk} = 0 if any of i,j,k are the same;
  • All other entries are obtained by counting how many times we exchanged two indices from \epsilon_{xyz} to get to them. For example, \epsilon_{xzy} is a single exchange, and so it is -1; \epsilon_{zxy} requires a second exchange and it is equal to +1.

So we find that in a two-state system, the operator for any physical observable can be built from a combination of the Pauli matrices and the identity matrix. Of course, this is only one “basis” - we could have chosen other matrices. I’ve used the Pauli matrices specifically because in systems involving spin, like the Stern-Gerlach system, they correspond naturally to physical observations of spin.

CautionOperator basis for qubits

In the quantum computing/quantum information literature, the Pauli basis is often used but written differently: instead of \{\hat{1}, \hat{\sigma}_x, \hat{\sigma}_y, \hat{\sigma}_z\}, the common notation is \{\hat{I}, \hat{X}, \hat{Y}, \hat{Z}\} (or often without the hats.)

When studying quantum circuits, the question of writing down an arbitrary operator is also very interesting, since it defines the minimal set of operators to build a universal quantum computer (such a set is called “universal quantum gate set”). This is a somewhat different problem from the one we solved, since for a quantum circuit the operators are applied one at a time in sequence, so we want to build an arbitrary \hat{O} from products of operators instead of adding them up.

Going into universal quantum gate sets is too much of a detour here, especially since quantum computing necessarily involves at least two qubits to make it interesting. Instead I will just note that when we want to form arbitrary operators from products of matrices, we need to introduce more special 2x2 matrices; some operators worth knowing about in the context of quantum computing are the Hadamard gate \hat{H}, and the \hat{S} and \hat{T} gates (examples of “phase gates”), defined as \hat{H} \equiv \frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right);\ \ \hat{S} \equiv \left( \begin{array}{cc} 1 & 0 \\ 0 & i \end{array}\right);\ \ \hat{T} \equiv \left( \begin{array}{cc} 1 & 0 \\ 0 & e^{i\pi/4} \end{array}\right).

3.2 Stern-Gerlach as a two-state system

Now that we have the mathematical ingredients - states on the Bloch sphere and observables built from Pauli matrices - let’s see how they map concretely onto our example Stern-Gerlach experiment. We’ll adopt the usual convention and identify our basis states \ket{\uparrow} and \ket{\downarrow} as the corresponding outputs from SG(\hat{z}). As we discussed, these outputs correspond to values of \pm \hbar/2 for the \hat{z}-component of the spin of the atoms, \hat{S}_z. From the postulates, this means that \ket{\uparrow}, \ket{\downarrow} as measurement outcomes are eigenstates of \hat{S}_z, and we also know the eigenvalues:

\hat{S}_z \ket{\uparrow} = +\tfrac{\hbar}{2} \ket{\uparrow}; \\ \hat{S}_z \ket{\downarrow} = -\tfrac{\hbar}{2} \ket{\downarrow}.

Looking back at our Pauli matrices, which have been defined in suggestive notation, we can immediately see that in matrix form, \hat{S}_z = \frac{\hbar}{2} \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) = \frac{\hbar}{2} \hat{\sigma}_z. (Convince yourself that the off-diagonal entries are zero, either mathematically or from the experiment!)

So far, so good; now let’s consider the other spin directions. Here’s one of the sequential configurations we looked at before:

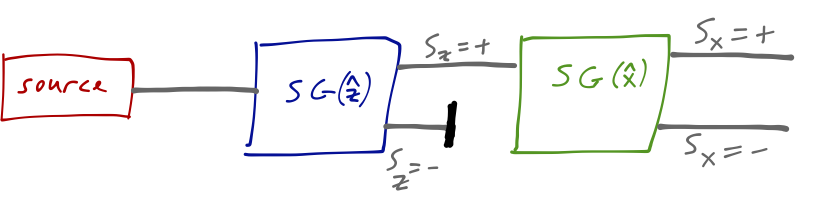
Sequential z-x Stern-Gerlach experiment.

On the final screen to the right, we again find two spots of equal intensity, corresponding to S_x = \pm \hbar/2. We also know that the outputs at the final screen are now eigenstates of \hat{S}_x and not of \hat{S}_z. Let’s denote the x-direction eigenstates as \ket{S_{x,+}} and \ket{S_{x,-}}. Then from Born’s rule, |\left\langle \uparrow | S_{x,+} \right\rangle| = |\left\langle \uparrow | S_{x,-} \right\rangle| = \frac{1}{\sqrt{2}}. This isn’t enough information to fix the x-direction states uniquely, but it tells us the coefficient of \ket{\uparrow} is 1/\sqrt{2} up to a phase.

Although I skipped to the answers a bit above, one can go through step by step and just use the results of Stern-Gerlach experiments to rigorously build up what all of the eigenstates have to look like, one constant at a time. I decided to cut this from my main notes in the interest of time, but I leave it here as an aside if you’re interested.

Continuing from the overlaps of \ket{\uparrow} with \ket{S_{x,\pm}} above, we get the same answers if we input \ket{\downarrow}, which tells us what the eigenkets of \hat{S_x} look like: \ket{S_{x,+}} = \frac{1}{\sqrt{2}} \ket{\uparrow} + \frac{1}{\sqrt{2}} e^{i \delta_1} \ket{\downarrow}, \\ \ket{S_{x,-}} = \frac{1}{\sqrt{2}} \ket{\uparrow} - \frac{1}{\sqrt{2}} e^{i \delta_1} \ket{\downarrow}. Actually, there is one more piece of information I’ve used here, which is that the kets are orthogonal: \left\langle S_{x,+} | S_{x,-} \right\rangle = 0. Once again, we can argue this mathematically (eigenstates with distinct eigenvalues are always orthogonal) or physically (we know that the probability of measuring S_x = - from the S_x = + beam is zero.)

Let’s put our work so far in terms of the Bloch sphere. The eigenstates of \hat{S}_z, \ket{\uparrow}, \ket{\downarrow}, exist at the north and south poles. Then the \hat{S}_x states we just found exist somewhere on the equator, with \theta = \pi/2, and they are also at equal and opposite points around the sphere (their phases \phi_{\pm} differ by exactly \pi.) But without further information, we can’t fix the final unknown phase \delta_1.

Is there any more information we can use to fix the extra phase factor? Remember that we can orient the S-G device in a third independent direction, along the y axis. In fact, we know that there is no difference between performing the sequential S-G experiment in the order z-x-z or z-y-z, which means that the construction of the \hat{S_y} eigenstates is basically identical, i.e. \ket{S_{y,+}} = \frac{1}{\sqrt{2}} \ket{\uparrow} + \frac{1}{\sqrt{2}} e^{i \delta_2} \ket{\downarrow}, \\ \ket{S_{y,-}} = \frac{1}{\sqrt{2}} \ket{\uparrow} - \frac{1}{\sqrt{2}} e^{i \delta_2} \ket{\downarrow}. We assign the \hat{S}_y eigenstates their own phase \delta_2, which can be different from \delta_1. In fact, it has to be different because we have another experimental input: we can perform the same sequential experiment using only x and y-direction S-G devices, which means that |\left\langle S_{y,\pm} | S_{x,+} \right\rangle| = |\left\langle S_{y,\pm} | S_{x,-} \right\rangle| = \frac{1}{\sqrt{2}}. Now we multiply out the kets we found above. For example, the product between both “+” components gives |\left\langle S_{y,+} | S_{x,+} \right\rangle| = \frac{1}{2} \left( 1 + e^{i(\delta_1 - \delta_2)} \right). Looking at all four products, we find two distinct equations, \left|1 \pm e^{i(\delta_1 - \delta_2)}\right| = \sqrt{2} the only solutions to which are \delta_1 - \delta_2 = \pm \frac{\pi}{2}.

Going back to the Bloch sphere, the final answer is more or less what you might have guessed: the states are maximally “spaced out”. The \hat{S}_x and \hat{S}_y eigenstates come in pairs on equal and opposite sides of the equator, and they are rotated \pi/2 relative to each other, so the four states form an equally-spaced ring around the equator. Note that this immediately means that, as I mentioned in the first lecture, it is impossible to make all of the kets real at the same time - we need complex numbers for even this very simple quantum system!

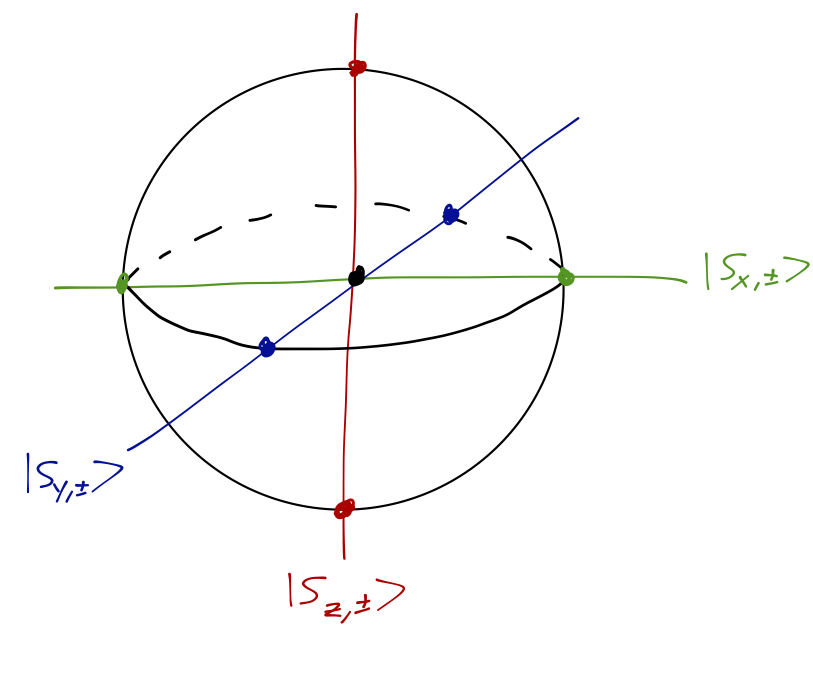
There are still, apparently, two ambiguities left in our total specification of the system: the value of \delta_1, and the sign of \delta_1 - \delta_2. We haven’t developed the machinery to consider symmetries, in particular changes in coordinate systems, just yet, but both of these choices amount to a choice of coordinates. It’s easiest to see this geometrically from the Bloch sphere: our \hat{S_z} eigenstates are at the poles, and \hat{S_x} and \hat{S_y} exist on the equator, equally spaced and separated by \phi = \pi/2.

It’s clear from the picture that choosing \delta_1 just amounts to choosing the position of the second coordinate axis (we’ve already forced one axis through the \hat{S_z} states on the poles.) The choice of sign for \delta_1 - \delta_2 is a convention, namely whether we are working in a left-handed or right-handed coordinate system. We’ll use standard right-handed coordinates in this class, which if we take \delta_1 = 0 gives \delta_2 = \pi/2 as the correct choice.

If we feed in all of the other experimental outcomes we know from Stern-Gerlach (see the aside above for all the details), all of the magnitudes and phases can be fixed, and we find the following results: \ket{S_{x,+}} = \frac{1}{\sqrt{2}} \ket{\uparrow} + \frac{1}{\sqrt{2}} \ket{\downarrow}, \\ \ket{S_{x,-}} = \frac{1}{\sqrt{2}} \ket{\uparrow} - \frac{1}{\sqrt{2}} \ket{\downarrow}, \\ \ket{S_{y,+}} = \frac{1}{\sqrt{2}} \ket{\uparrow} + \frac{i}{\sqrt{2}} \ket{\downarrow}, \\ \ket{S_{y,-}} = \frac{1}{\sqrt{2}} \ket{\uparrow} - \frac{i}{\sqrt{2}} \ket{\downarrow}. Since these states represent measurement outcomes, they must be eigenstates of the corresponding operators for \hat{S}_x and \hat{S}_y. Unsurprisingly, these operators are exactly just the Pauli matrices times \hbar/2:

\hat{S}_x = \frac{\hbar}{2} \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right) = \frac{\hbar}{2} \hat{\sigma}_x \\ \hat{S}_y = \frac{\hbar}{2} \left( \begin{array}{cc} 0 & -i \\ i & 0 \end{array} \right) = \frac{\hbar}{2} \hat{\sigma}_y \\ \hat{S}_z = \frac{\hbar}{2} \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right) = \frac{\hbar}{2} \hat{\sigma}_z.

The overall statement is that the vector spin operator \hat{\vec{S}} = \tfrac{\hbar}{2} \hat{\vec{\sigma}}.

Bloch sphere with all 3 axes included.
NoteExercise: building \hat{S}_{x,y}

Knowing the eigenstates and eigenvalues from above is all we need to build the corresponding operators; find \hat{S}_x and \hat{S}_y.

Answer:

We begin with \hat{S}_x. If we know the eigenvectors, we can build a matrix from outer products: \hat{S_x} = \frac{\hbar}{2} \ket{S_{x,+}} \bra{S_{x,+}} - \frac{\hbar}{2} \ket{S_{x,-}} \bra{S_{x,-}} \\ = \frac{\hbar}{4} \left( (\ket{\uparrow} + \ket{\downarrow}) (\bra{\uparrow} + \bra{\downarrow}) - (\ket{\uparrow} - \ket{\downarrow}) (\bra{\uparrow} - \bra{\downarrow}) \right) \\ = \frac{\hbar}{4} \left( 2 \ket{\uparrow} \bra{\downarrow} + 2 \ket{\downarrow} \bra{\uparrow} \right) \\ = \frac{\hbar}{2} \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right).

For \hat{S_y}, everything is very similar, but the complex conjugation on the bras gives some extra signs. Going slowly: \hat{S_y} = \frac{\hbar}{2} \ket{S_{y,+}} \bra{S_{y,+}} - \frac{\hbar}{2} \ket{S_{y,-}} \bra{S_{y,-}} \\ = \frac{\hbar}{4} \left( (\ket{\uparrow} + i\ket{\downarrow}) (\bra{\uparrow} - i\bra{\downarrow}) - (\ket{\uparrow} - i\ket{\downarrow})(\bra{\uparrow} + i\bra{\downarrow}) \right) \\ = \frac{\hbar}{4} \left( -2i \ket{\uparrow} \bra{\downarrow} + 2i \ket{\downarrow} \bra{\uparrow} \right) \\ = \frac{\hbar}{2} \left( \begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right).

No surprise that we ended up with the other two Pauli matrices!

You can also double-check the algebra here by going backwards: computing the eigenvectors and eigenvalues of the matrices we obtained in the usual way, and making sure we reconstruct the vectors that we started with.

With the phases all fixed, we have for our final set of three operators exactly just the Pauli matrices times \hbar/2:

3.3 Commutation and compatible observables

As I hinted before, the commutator is a particularly interesting property to look at between operators. We’ve seen in the Stern-Gerlach experiment that the order in which we apply measurements matters: for example, projecting upper components in the order S_{z,+}, S_{x,+}, S_{z,-} gives a non-zero signal, but reversing the order to S_{z,+}, S_{z,-},S_{x,+} does not.

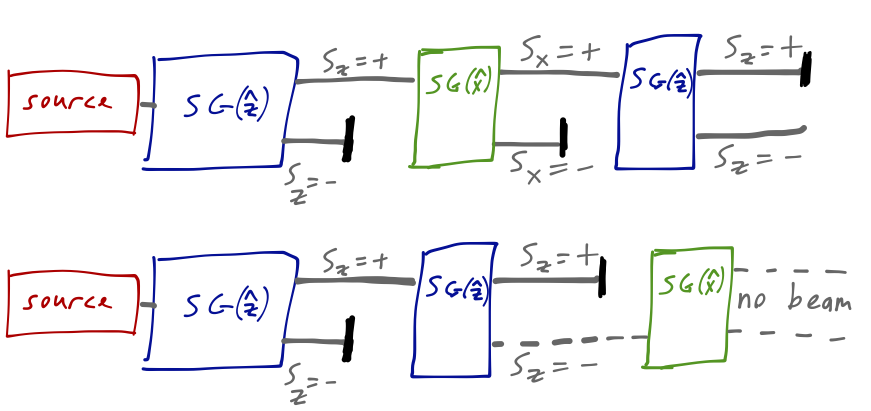
Two different measurement orders for a Stern-Gerlach experiment.

This non-commutation of measurements is easy to see in the operator formalism. We know that when we make a measurement, the state of the system collapses into one of the eigenstates of whatever operator we observe, for example \hat{S_z} \ket{\psi} \rightarrow \pm \frac{\hbar}{2} \ket{S_{z,\pm}}. Clearly if we perform the same measurement again (ignoring time evolution of the state itself, which we’ll get to), Born’s rule tells us that we find the same eigenvalue with probability 1. We can see this clearly in the sequential case sketched above with two SG(\hat{z}) measurements in a row.

However, if we perform a different measurement, we won’t get a guaranteed outcome anymore. Moreover, we can see that the order of measurement matters, from the sketch above: \hat{S_x} \hat{S_z} \ket{\uparrow} \neq \hat{S_z} \hat{S_x} \ket{\uparrow} \Rightarrow [\hat{S_x}, \hat{S_z}] \ket{\uparrow} \neq 0. In other words, experimentally, the observables \hat{S_x} and \hat{S_z} do not commute - and in fact, this is true for any state, not just \ket{\uparrow}. From our work above, you can easily verify that this is true algebraically, simply because the commutator [\hat{\sigma}_x, \hat{\sigma}_z] \neq 0.

What if we had two operators that did commute with each other? In general, if [\hat{A}, \hat{B}] = 0, we say that \hat{A} and \hat{B} are compatible operators. But let’s think about what that implies: we know for any state \ket{\psi}, that \hat{A} \hat{B} \ket{\psi} = \hat{B} \hat{A} \ket{\psi}. Now suppose that \ket{\psi} is an eigenstate of \hat{A}, call it \ket{a}. If we measure \hat{A} first, then we get outcome a with 100% probability. But because the operators commute, if we measure \hat{B} first, we still get outcome a for \hat{A} with 100% probability. You can convince yourself that the only way this can be true is if the eigenstates \ket{b} of \hat{B} are also eigenstates of \hat{A}, and vice-versa: so we can label all of the measurement outcomes as \ket{a,b}. Algebraically, this is the statement that \hat{A} and \hat{B} are simultaneously diagonalizable - we can find a basis of states that are eigenstates of both at once.

For those who are more mathematically inclined, here’s a quick proof of the statement above with some assumptions. If the eigenvalues of \hat{A} are non-degenerate, then in the basis of eigenkets \{ \ket{a}\}, a compatible operator \hat{B} is represented by a diagonal matrix. (Obviously, so is \hat{A}.) This is straightforward to see: \bra{a_j} [\hat{A}, \hat{B}] \ket{a_i} = \bra{a_j} (\hat{A} \hat{B} - \hat{B} \hat{A}) \ket{a_i} \\ = \sum_{k} \bra{a_j} \hat{A} \ket{a_k} \bra{a_k} \hat{B} \ket{a_i} - a_i \bra{a_j} \hat{B} \ket{a_i} \\ = \sum_{k} a_k \delta_{jk} \bra{a_k} \hat{B} \ket{a_i} - a_i \bra{a_j} \hat{B} \ket{a_i} \\ = (a_j - a_i) \bra{a_j} \hat{B} \ket{a_i} = 0. Since we assumed the eigenvalues of \hat{A} are non-degenerate, then if i \neq j the matrix element of \hat{B} is zero. So \hat{B} is diagonal.

Dealing with the degenerate case, where there can be eigenvalues of \hat{A} which appear repeatedly, is more complicated - but it can be done, and it is in fact generally true that if [\hat{A}, \hat{B}] = 0, there exists a basis in which the operators are simultaneously diagonalized. Although I won’t prove it, this also goes the other way: simultaneously diagonalizable operators must always commute with each other.

We’ll come back to a more general discussion of compatible operators and simultaneous diagonalization later on. For the two-state system, things are very constrained: we know that none of the spin-component operators \hat{S_x}, \hat{S_y}, \hat{S_z} commute with one another. The only thing that can commute is the identity operator \hat{1}, and in fact this does correspond to a physical observable, which is the square of the spin vector: \hat{\mathbf{S}}{}^2 \equiv \hat{S_x}{}^2 + \hat{S_y}{}^2 + \hat{S_z}{}^2 = \frac{3}{4} \hbar^2 \hat{1}, where we’ve used the properties of the Pauli matrices to show that this operator is proportional to the identity operator. Clearly, this implies that [\hat{\mathbf{S}}{}^2, \hat{S_i}] = 0 and the eigenstates of any of the \hat{S_i} are also eigenstates of \hat{\mathbf{S}}{}^2. But this is trivial in this case: the identity operator always gives us the same outcome for any state. As we will see later, for systems with higher spin \hat{\mathbf{S}}{}^2 will become more interesting.

3.4 The uncertainty relation

If two observables are not compatible, [\hat{A}, \hat{B}] \neq 0, then they do not have simultaneous eigenstates: we can’t precisely know the values of both observables simultaneously. What we can do is make statistical statements; given an ensemble in some state \ket{\psi} and many repeated trials, we can determine the expectation values \left\langle \hat{A} \right\rangle and \left\langle \hat{B} \right\rangle.

But it turns out that even when we’re willing to back off to statistical measurements of an ensemble, there is still a fundamental limit on how precisely we can predict the outcomes of incompatible observables. You have seen this before in the form of the Heisenberg uncertainty principle for momentum and position of a particle. Here we consider a more general inequality known as the uncertainty relation.

For this derivation, we first define an operator \Delta \hat{A} \equiv \hat{A} - \left\langle \hat{A} \right\rangle which measures the residual difference between the outcome of \hat{A} and the expected mean. The expectation value of the square of this difference is called the variance or the dispersion: (\Delta A)^2 \equiv \left\langle (\Delta \hat{A})^2 \right\rangle = \left\langle \left(\hat{A}^2 - 2 \hat{A} \left\langle \hat{A} \right\rangle + \left\langle \hat{A} \right\rangle^2 \right) \right\rangle = \left\langle \hat{A}^2 \right\rangle - \left\langle \hat{A} \right\rangle^2. (Note: watch where the hats are located! The quantity \Delta \hat{A} is an operator, but the variance (\Delta A)^2 is defined from expectation values and so is just a number.)

This dispersion measures how widely dispersed the results of measuring \hat{A} will be over many trials. In fact, by the central limit theorem, if we repeat our experiment an enormous number of times the distribution will be a Gaussian, centered at \left\langle \hat{A} \right\rangle and with 68% of the observations within one standard deviation \Delta A of \left\langle \hat{A} \right\rangle.

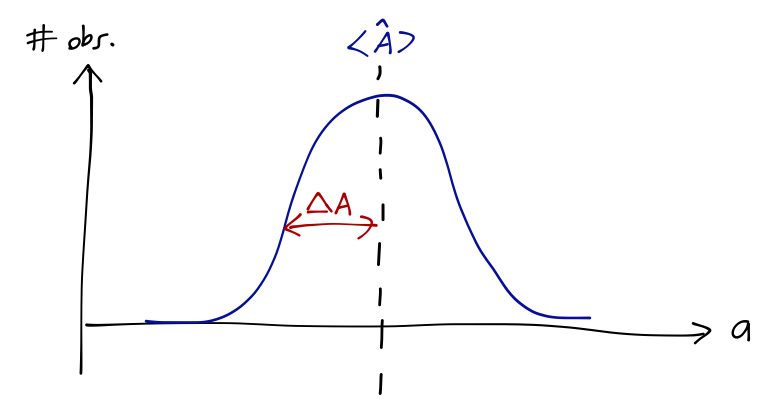
We know that there are some experiments for which the dispersion will be zero; if we prepare a pure eigenstate \ket{a} of \hat{A}, then we will always measure the same eigenvalue a. However, for a more general state there will be some dispersion. In particular, even if our system is in an eigenstate of \hat{A}, we might expect to find some dispersion if we measure an incompatible observable \hat{B}. For example, if we go back to our Stern-Gerlach system and prepare an eigenstate \ket{\uparrow} of \hat{S_z}, then \Delta S_z = 0, but if we try to measure \hat{S_x}, we find that \Delta S_x = \sqrt{\left\langle \hat{S_x}^2 \right\rangle - \left\langle \hat{S_x} \right\rangle^2} = \frac{\hbar}{2}. If we choose a different state, the dispersions of \hat{S_x} and \hat{S_z} will be different, but they can never both be made arbitrarily small; there is a limit on the combination of the two.

ImportantThe uncertainty relation

For any state and any two observables \hat{A} and \hat{B}, their variances must satisfy the uncertainty relation,

(\Delta A) (\Delta B) \geq \frac{1}{2} \left| \left\langle [\hat{A}, \hat{B}] \right\rangle\right|.

Let’s prove this inequality. Our starting point is the Cauchy-Schwarz inequality: if we let \ket{\alpha} = \Delta \hat{A} \ket{\psi} \\ \ket{\beta} = \Delta \hat{B} \ket{\psi} where \ket{\psi} is arbitrary, then the inequality gives us \left\langle \alpha | \alpha \right\rangle \left\langle \beta | \beta \right\rangle \geq |\left\langle \alpha | \beta \right\rangle|^2 \\ \Rightarrow \bra{\psi}(\Delta \hat{A})^2 \ket{\psi} \bra{\psi} (\Delta \hat{B})^2 \ket{\psi} \geq |\bra{\psi} (\Delta \hat{A}) (\Delta \hat{B}) \ket{\psi}|^2. Now we’ll use a useful trick: we can rewrite the product of two operators like so, \Delta \hat{A} \Delta \hat{B} = \frac{1}{2} [\Delta \hat{A}, \Delta \hat{B}] + \frac{1}{2} \{ \Delta \hat{A}, \Delta \hat{B}\}. (If it’s not obvious this is true, expand out and convince yourself!) We know that the observables themselves are Hermitian, but what about the commutator and anti-commutator? Well, first notice that [\Delta \hat{A}, \Delta \hat{B}] = [\hat{A} - \left\langle \hat{A} \right\rangle, \hat{B} - \left\langle \hat{B} \right\rangle] = [\hat{A}, \hat{B}] since the commutator vanishes if either argument is a scalar. This commutator is anti-Hermitian: ([\hat{A}, \hat{B}])^\dagger = (\hat{A} \hat{B} - \hat{B} \hat{A})^\dagger \\ = \hat{B}^\dagger \hat{A}^\dagger - \hat{A}^\dagger \hat{B}^\dagger \\ = \hat{B} \hat{A} - \hat{A} \hat{B} \\ = - [\hat{A}, \hat{B}]. Just like the expectation value of any Hermitian operator is real, that of an anti-Hermitian operator is purely imaginary. On the other hand, it’s easy to show that the anticommutator \{\Delta \hat{A}, \Delta \hat{B}\} is in fact Hermitian. So we’ve rewritten the object inside the absolute value above as a real part and an imaginary part, which means that the absolute value is just the sum of the squares: \left|\left\langle \Delta \hat{A} \Delta \hat{B} \right\rangle\right|^2 = \frac{1}{4} \left| \left\langle [\hat{A}, \hat{B}] \right\rangle \right|^2 + \frac{1}{4} \left| \left\langle \{\Delta \hat{A}, \Delta \hat{B}\} \right\rangle \right|^2 Since the anticommutator term is always positive, this is always greater than or equal to \frac{1}{4} \left| \left\langle [\hat{A}, \hat{B}] \right\rangle \right|^2, so our proof is complete; taking the square root of both sides gives the form of the relation written above.

Coming back to the two-state system: for any two spin-component observables, we have [\hat{S}_i, \hat{S}_j] = \frac{\hbar^2}{4} [\hat{\sigma}_i, \hat{\sigma}_j] = \frac{\hbar^2}{4} (2i \epsilon_{ijk} \hat{\sigma}_k) = i\hbar \epsilon_{ijk} \hat{S}_k. So concretely, we see that for example, \Delta S_x \Delta S_z \geq \frac{1}{2} \left| \left\langle [\hat{S}_x, \hat{S}_z] \right\rangle \right| = \frac{\hbar}{2} \left| \left\langle \hat{S_y} \right\rangle \right|. As we saw above, it is possible to have zero uncertainty on one of the measurements: if we prepare an eigenstate of \hat{S_z} like \ket{\uparrow}, then \Delta S_z = 0. This doesn’t violate the uncertainty relation, because in that particular state \left\langle \hat{S_y} \right\rangle = 0 as well. But eigenstates are special, and since \hat{S}_x and \hat{S}_z don’t commute, it turns out to be impossible to also have \Delta S_x = 0 at the same time. If we insist on building states that are not eigenstate of either \hat{S}_x or \hat{S_z}, then both variances will be non-zero, but we will find that the uncertainty relation limits how we can construct such a state.

We can use the Bloch sphere parameterization above to picture what is going on, usefully. In the \hat{S}_z basis, the state \ket{\uparrow} is at the north pole, with \left\langle \hat{S}_x \right\rangle = \left\langle \hat{S}_y \right\rangle = 0. But the reason it has zero expectation in those other two directions is because it is maximally mixed between the two eigenstates \ket{S_{x,\pm}}, or equivalently \ket{S_{y,\pm}}. So minimal uncertainty in the z-direction gives maximal uncertainty in the other two directions (and all consistent with the three uncertainty relations we could write out, as you can easily check.)