9 Symmetry in quantum mechanics
The concept of symmetry is extremely important and useful in pretty much every kind of physics. Symmetries constrain the ways in which our system can exist and evolve; taking them into account can often greatly simplify our calculations (and indeed, they cannot be avoided: even if we solve a problem the “hard way”, the presence of symmetry can reveal itself in the form of unexpected simplicity or patterns occuring in our answers!)
The basic idea of a symmetry is that it is a way that our physical system can be changed while preserving certain features. At the beginning of this course when considering the Stern-Gerlach experiment, we noted that the x,y,z direction labels are somewhat arbitrary; if we put an unpolarized beam of silver atoms through a Stern-Gerlach analyzer oriented in any of these directions (or indeed, any spatial direction at all!), we will get the same outcome: two split beams of equal intensity. This reflects the presence of rotational symmetry in the system.
Of course, you should be familiar with symmetry in other physical systems, so let’s talk about how symmetries show up in quantum mechanics in particular. Using our Hilbert space notation, we can imagine that “changing the system” corresponds to some transformation operator \hat{T} that we can construct. Then suppose that our “physical system” consists of a set of states \ket{\psi} and observables \hat{A} with eigenstates \{\ket{a}\}.
With this setup, the statement of symmetry that “changing our system leaves the physics unchanged” can be given more concretely as follows:
- The transformation \hat{T} acts on all states in our physical system, transforming them as \ket{\psi} \rightarrow \hat{T} \ket{\psi} and \ket{a} \rightarrow \hat{T} \ket{a}.
- If \hat{T} is a symmetry of a particular Hilbert space, then all physical statements before and after applying \hat{T} must be the same.
- By Born’s rule, the probability of observing outcome a from state \ket{\psi} is |\left\langle a | \psi \right\rangle|^2. This must be invariant under \hat{T} if it is a symmetry, so we find |\bra{a} \hat{T}{}^\dagger \hat{T} \ket{\psi}|^2 = |\left\langle a | \psi \right\rangle|^2 for any a and any \ket{\psi}.
This almost guarantees that a symmetry operator \hat{T} must be unitary. In fact, the argument above gives the essential content of a useful result which I won’t attempt to rigorously prove here:
Any transformation \hat{T} of a quantum mechanical system that describes a symmetry is either unitary or anti-unitary.
We haven’t defined anti-unitary operator yet: an anti-unitary \hat{T} satisfies the odd-looking property \bra{x} \hat{T}{}^\dagger \hat{T} \ket{y} = \left\langle y | x \right\rangle. Almost every symmetry in quantum mechanics is unitary, the most important anti-unitary example being the somewhat esoteric time-reversal symmetry, which we’ll come back to much later (since it implies interesting facts that depend on things we haven’t studied yet.)
One thing to emphasize about this result is that we haven’t specified what \hat{T} does to the states it acts on; they could be eigenstates of \hat{T}, picking up a phase, or they could be mapped into different states, or \hat{T} might do nothing at all. One possibility is the global phase symmetry we already pointed out, where \hat{T} = e^{i\phi} \hat{1} acting on all states. This is a good symmetry by the definition above, but it also doesn’t really tell us anything interesting! The more interesting symmetries are the ones where different states map differently under \hat{T}, but nevertheless, the physics outcomes are the same.
It’s also worth remarking that it’s possible (and often useful) to think of the transformation as acting on the operators of our physical system, instead of the states. This comes from thinking about how the expectation value of some operator \hat{A} transforms under our symmetry: \left\langle \hat{A} \right\rangle = \bra{\psi} \hat{A} \ket{\psi} \rightarrow \bra{\psi} \hat{T}^\dagger \hat{A} \hat{T} \ket{\psi}. This gives us an alternative way of describing the action of the transformation \hat{T}: we can describe it as acting on the operators in our system as \hat{A} \rightarrow \hat{T}^\dagger \hat{A} \hat{T}. Note that this is just a different “picture” again, active vs. passive transformation: you should not try to transform both operators and states (basis vectors) at the same time, only one or the other! This second picture does let us clearly see how specific operators are affected by the transformation, and in particular, we see that \hat{A} is invariant (or “preserves the symmetry”) only if \hat{A} = \hat{T}^\dagger \hat{A} \hat{T}; given that we know \hat{T} is (almost always) unitary, then this is equivalent to \hat{T} \hat{A} = \hat{A} \hat{T} \\ \Rightarrow [\hat{A}, \hat{T}] = 0. By the definition above, \hat{T} is a symmetry only if [\hat{A}, \hat{T}] = 0 for all physical observables \hat{A}.
9.0.1 Dynamical symmetry
One operator in particular is usually especially important when considering symmetry: the Hamiltonian \hat{H}, which governs time evolution. If our Hamiltonian doesn’t preserve the symmetry \hat{T}, then even if we start in a symmetric state, the symmetry will not be conserved at later times as our system evolves.
Let’s make this statement about time evolution more concrete. Suppose that at t=0, our system begins in state \ket{\psi(0)}, and \hat{T} is a good symmetry. Then the time-evolved state is \ket{\psi(t)} = \hat{U}(t) \ket{\psi(0)} = \exp \left( \frac{-i \hat{H} t}{\hbar} \right) \ket{\psi(0)}.
Then we measure \hat{A} and find outcome \ket{a}. The probability at time zero is p_a(t=0) = |\left\langle a | \psi(0) \right\rangle|^2 \rightarrow |\bra{a} \hat{T}^\dagger \hat{T} \ket{\psi(0)}|^2 which is a good symmetry for \hat{T} satisfying Wigner’s theorem. But then at a later time, we have p_a(t) = |\left\langle a | \psi(t) \right\rangle|^2 = |\bra{a} \hat{U}(t) \ket{\psi(0)}|^2 \\ \rightarrow |\bra{a} \hat{T}^\dagger \hat{U}(t) \hat{T} \ket{\psi(0)}|^2, since we only know how the symmetry acts on the initial state \ket{\psi(0)}. But now for the symmetry to still be good, we have to be able to commute \hat{T} with the time evolution operator, which means we must have [\hat{U}(t), \hat{T}] = 0, and since we want this to be true for all possible times t, this means that [\hat{H}, \hat{T}] = 0.
Connecting to our discussion above about operators, this condition tells us that conjugating the Hamiltonian by \hat{T} should leave it unchanged: rearranging to get \hat{H} \hat{T} = \hat{T} \hat{H} and then multiplying either on the left or right by \hat{T}^\dagger, we find that \hat{T} \hat{H} \hat{T}^\dagger = \hat{T}^\dagger \hat{H} \hat{T} = \hat{H}. As we’ve noted before, the commutation condition also tells us that \hat{T} and \hat{H} are simultaneously diagonalizable. This means that we can find a set of combined eigenstates \ket{t, E}, or alternatively, we can label and classify energy eigenstates according to their eigenvalues under the transformation \hat{T} - which is often quite useful, as we will see in another wave mechanics example shortly.
A transformation \hat{T} is a dynamical symmetry of a quantum system if [\hat{T}, \hat{H}] = 0.
It is worth remarking on a fine point here that many references take for granted, which has to do with how we define symmetry. With the Wigner’s theorem definition above, we state that all physics is invariant under the transformation \hat{T}. This is very useful for certain foundational symmetries, things like translation invariance - the observation that if we move our entire experimental apparatus somewhere else in space, we should get the same results.
However, it’s common for a transformation to only leave parts of our system invariant. If we have a sphere in our laboratory, it is true that the Universe is rotationally invariant under moving the entire lab and the Earth around. But it’s also true that rotations of only the sphere about its center leave the experiment invariant, and these are separate operations. So we will talk about symmetries under which parts of our system are invariant - we’ll see an example soon.
As an example, if we have a dynamical symmetry \hat{T}, then even if our initial state \ket{\psi(0)} is not symmetric, we can always decompose it usefully into components which are symmetric, \ket{\psi(0)} = \sum_{(t,E)} c_{t,E} \ket{t,E}. Isolating and solving for the symmetry-labelled eigenstates can often be simpler than solving the more general problem, as we will see below.
So far, everything I’ve said has been very general, applying to all sorts of symmetries. We’ll begin our study of symmetry with examples of discrete symmetries, which are symmetries that have a finite spectrum of eigenvalues. This in turns lets us classify the states of our system into a finite list of subsets based on their symmetry eigenvalues. The case of continuous symmetry with an infinite number of eigenvalues is also important, but we’ll put that off for the moment.
This is probably as far as it is useful to go with general definitions, for now: let’s move on to something more concrete.
9.1 Parity
A simple yet powerful symmetry that we can study is parity, also known as mirror reflection. Parity flips our coordinate system backwards: in one dimension, it takes x \rightarrow -x and p \rightarrow -p. (It will, in general, reverse the sign of any vector quantity - we just don’t usually label vectors explicitly in one dimension, so we need to be a little careful! Even though we’re in 1-d at the moment, I’m going to write x as \vec{x} for a bit - this also makes it easy to generalize what I will say to higher dimensions.)
In quantum mechanics, we construct a parity operator \hat{P} that accomplishes this transformation. We will start in the operator picture and define it in terms of how it acts on our operators: for example, for the position operator it must act as \hat{P}{}^\dagger \hat{\vec{x}} \hat{P} = -\hat{\vec{x}} (and the same for \hat{\vec{p}} or any other vector operator, as noted.)
The parity operator has to be unitary: we can see that by applying it to the dot product of two vectors, which should itself be invariant under parity: \hat{P}{}^\dagger \hat{\vec{x}} \hat{P} \cdot \hat{P}{}^\dagger \hat{\vec{x}} \hat{P} = \hat{\vec{x}} \cdot \hat{\vec{x}} = \hat{P}{}^\dagger (\hat{\vec{x}} \cdot \hat{\vec{x}}) \hat{P} so \hat{P}{}^\dagger = \hat{P}{}^{-1}, i.e. \hat{P} is unitary (as it should be to describe a symmetry.)
Going back towards wave mechanics, what does parity do to our wavefunctions? This is more useful to think about in the passive transformation picture where our states change instead of our operators. We can relate the two by writing \bra{\vec{x}'} \hat{\vec{x}} \ket{\vec{x}} \rightarrow \bra{\vec{x}'} \hat{P}^\dagger \hat{\vec{x}} \hat{P} \ket{\vec{x}} \\ = \bra{\vec{x}'} -\hat{\vec{x}} \ket{\vec{x}} = - \vec{x} \delta(\vec{x} - \vec{x}') = -\vec{x}' \delta(\vec{x} - \vec{x}') so we see that (as we might have guessed) parity is flipping the sign of our position eigenvalues, \hat{P} \ket{\vec{x}} = \ket{-\vec{x}}.
This means that the wavefunction transforms as \psi(\vec{x}) = \left\langle \vec{x} | \psi \right\rangle \rightarrow \bra{\vec{x}} \hat{P} \ket{\psi} = \left\langle -\vec{x} | \psi \right\rangle = \psi(-\vec{x}). In fact, from the states it’s easy to see that \hat{P} is more than just unitary: if we apply parity twice, then \hat{P}^2 \ket{\vec{x}} = \hat{P} \ket{-\vec{x}} = \ket{+\vec{x}} so we also have \hat{P}{}^2 = \hat{1}; in other words, \hat{P} is its own inverse. (If you are familiar with group theory, this last property indicates that the symmetry group associated with parity is \mathbb{Z}_2. More on symmetry and groups later on.)
What do the parity eigenstates look like? If \ket{P} is a parity eigenstate, then we have \hat{P} \ket{P} = P \ket{P}. But \hat{P}{}^2 \ket{P} = P \hat{P} \ket{P} = P^2 \ket{P} = \ket{P} so P^2 = 1, i.e. the eigenvalues of parity are always P = \pm 1.
The action of parity on the Hamiltonian is particularly interesting. If we find parity is a dynamical symmetry, i.e. [\hat{P}, \hat{H}] = 0, then we will be able to construct simultaneous eigenkets of \hat{P} and \hat{H}. The momentum part of the Hamiltonian is proportional to \vec{p} \cdot \vec{p}, and as we saw above, the dot product of a vector with itself is parity invariant, so \hat{H} is invariant if the potential is invariant, V(\vec{x}) = V(-\vec{x}). For a potential satisfying this condition (like our square well), any eigenket of \hat{H} is also an eigenket of \hat{P}.
Any energy eigenfunction \psi(x) can therefore be identified as either a positive-parity or even state, with P=1, or a negative-parity or odd state with P=-1. We can see what this implies for the spatial wavefunctions: if \ket{\psi} is an energy/parity eigenstate, then \left\langle x | \psi \right\rangle = \bra{x} \hat{P} \hat{P} \ket{\psi} = P \left\langle -x | \psi \right\rangle. So in other words, the even-parity wavefunctions satisfy \psi_e(\vec{x}) = \psi_e(-\vec{x}) and the odd-parity ones satisfy \psi_o(\vec{x}) = - \psi_o(-\vec{x}).
9.2 Example: the square well
Now that we have parity as a tool, let’s attack another simple wave mechanics example by taking our potential barrier and flipping it upside down, i.e. taking V_0 to -V_0; this gives us the square well potential: V(x) = \begin{cases} -V_0, & |x| < a \\ 0, & |x| > a. \end{cases}
We’ll begin with the case where -V_0 < E < 0, looking for bound states. If we let \epsilon = E + V_0 = V_0 - |E| be the distance between the energy and the bottom of the well, then the wave number inside the well is the usual k = \sqrt{2m\epsilon} / \hbar. The exponential decay constant outside the well is \kappa = \sqrt{2m|E|} / \hbar. The general solution looks like \psi(x) = \begin{cases} B_+ e^{+\kappa x}, & (x < -a); \\ A_+ e^{ikx} + A_- e^{-ikx}, & (-a < x < a); \\ B_- e^{-\kappa x}, & (x > a). \end{cases}
However, instead of solving this directly, we first notice that because the potential is symmetric in x, parity commutes with our Hamiltonian. Thus, we know that we can split the solutions into those with even parity, \psi_e(x) = \begin{cases} A \cos kx, & |x| < a; \\ B e^{-\kappa |x|}, & |x| > a. \end{cases}
and those with odd parity, \psi_o(x) = \begin{cases} A' \sin kx, & |x| < a; \\ B' e^{-\kappa x}, & x > a; \\ -B' e^{\kappa x}, & x < a. \end{cases}
So we’ve immediately reduced our unknown coefficients from 4 down to 2 for each subset of solutions. We’ve also reduced the number of constraints from continuity to 2, since continuity of \psi(x) and its derivative at x = +a now also guarantees it at the reflected boundary x = -a. There is one more constraint, overall normalization of the wavefunction; only certain values of the energy E will allow us to satisfy all constraints, as expected for bound states.
Let’s start with the even-parity solution. Applying the boundary condition at x=a (the other boundary is redundant thanks to parity!) to this state gives A \cos ka = B e^{-\kappa a} \\ -Ak \sin ka = -B\kappa e^{-\kappa a} which can be combined to obtain a condition on the wave numbers and thus the allowed energy E: ka \tan ka = \kappa a. Similarly, for the odd-parity states we find ka \cot ka = -\kappa a. Now let’s define for convenience the parameters \xi \equiv ka and \eta \equiv \kappa a. From the definitions of k and \kappa, we see that \xi^2 + \eta^2 = \frac{2ma^2}{\hbar^2} (E + V_0 - E) = \frac{2ma^2}{\hbar^2} V_0, while from above we have (for even parity) \xi \tan \xi = \eta. This is a transcendental equation, so we can’t find a closed-form solution. However, we can solve this pair of equations graphically. If we plot \eta vs. \xi, then the first equation above defined a circle with radius \sqrt{2mV_0} a/\hbar; solutions occur wherever this circle intersects the function \xi \tan \xi.
These are solutions for the bound-state energy E, which determines the values of k and \kappa. Notice that even as the radius of the circle vanishes, we will always find at least one even-parity bound state. As the radius rises (the well becomes deeper or wider), the number of solutions increases. If we take V_0 \rightarrow \infty then we find an infinite number of bound-state solutions, corresponding to the (even-parity) standard results for the infinite square well.
What about the odd-parity solutions? We have the same equation for the circular curves, but now the boundary conditions instead yield the relation \xi \cot \xi = -\eta.
Now we see that there will be no solutions if \sqrt{2mV_0} a/\hbar < \pi/2; if the potential well is too shallow, there are no odd-parity bound states.
For completeness, I’ll note that we can also study scattering from the square well, i.e. solutions with E>0. We will find similar results to what we had for the barrier before: I won’t go through the details, but in particular we find for the transmission coefficient T = \left(1 + \frac{\sin^2(2k'a)}{4E/V_0(E/V_0+1)} \right)^{-1}. so we once again have resonance at precisely the values 2k'a = n\pi. (However, note that the definition of k' has changed: for the potential barrier we had k' = \sqrt{2m(E-V_0)}/\hbar, while for the well it is k' = \sqrt{2m(E+V_0)}/\hbar.)
We can think about this more physically to understand the source of the resonant behavior. Remember that at any barrier, a quantum-mechanical particle will undergo both transmission and reflection (this is possible because the wavefunction allows a single particle to be non-localized in a sensible way.) Although we’ve focused on the final transmission amplitude, there is generically transmission and reflection at both edges of the barrier. In particular, some part of the incident plane wave A will be reflected internally some number of times before finally being transmitted into outgoing wave F. The condition 2k'a = n\pi can be rewritten as 4a = n (2\pi/k'), in other words, transmission resonance occurs when the distance 4a traveled by an internally reflected wave is equal to an integer multiple of the de Broglie wavelength (2\pi/k'), resulting in constructive interference.
9.3 Symmetry and groups
Let’s step back into formalism again and develop a little bit more mathematics that will be very useful, especially for our future studies of more complicated symmetries.
We begin with the idea of a group. A group is a collection of some objects (a set), together with a product operation \cdot which satisfies the following rules:
- Closure: (a \cdot b) is still in the group
- Associativity: a \cdot (b \cdot c) = (a \cdot b) \cdot c
- Identity: the group contains 1 so that (1 \cdot a) = (a \cdot 1) = a
- Inverse: each a has another element a^{-1} satisfying a^{-1} \cdot a = a \cdot a^{-1} = 1.
These are, in fact, exactly the natural rules to describe a symmetry in physics. In a very high-level sense, a symmetry means that there are different “points of view” under which a physical system is the same - equivalent descriptions of the same object. (For example, we often think of parity as an active transformation - mirror reflection - but it’s just as good to take the passive picture and observe that parity symmetry means the system has the same coordinates when we turn our coordinate axes backwards.) In this more abstract point of view, there are some obvious properties that we need:
A. If we change our point of view twice, we should get another point of view of the same system; B. We should be able to switch freely between points of view, since they are equivalent descriptions; in particular, if we can change from POV A to B, we should also be able to change from B to A.
If you think about what these properties imply, it should be obvious that they map nicely onto the structure of a group: A tells us we want a set and a product operation with closure, and B tells us that we should have an inverse and therefore also an identity. (Associativity is sort of a technical property that comes along for the ride, without which our order of operations would get weird.) So, symmetries in physics are naturally described in terms of symmetry groups.
As an exercise in literal “points of view”, let’s consider the symmetry group of rotations by (multiples of) 90 degrees in two dimensions. Thinking of this as a coordinate transformation, we have four “points of view” - that is, four directions in which the positive x axis can be pointing.
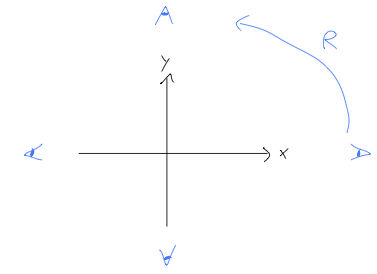
To reveal the group structure, let’s call R the group element corresponding to a single counter-clockwise rotation by 90 degrees.
Applying R \cdot R gives us a rotation by 180 degrees, another element of the group; instead of introducing another letter, we can just call this element R^2. Similarly, R^2 \cdot R = R^3 is a rotation by 270 degrees. Finally, R^3 \cdot R = 1; if we rotate by 360 degrees, we come back to where we started, i.e. the identity. We see evidently that the group is closed; moreover, every element of the group matches on to one of the four points of view we identified to start with.
We also need an inverse operation, which is simply provided by rotating clockwise: following the notation above, we could call this element R^{-1}, but you can easily convince yourself that R^{-1} is just R^3, the 270-degree counter-clockwise rotation. In fact, we have already written down all of the group elements - which is good, because we already have four of them, and if there was a fifth then there would have to be a fifth point of view that we have missed so far!
So, the discrete 2d rotation group is the set of elements \{1, R, R^2, R^3\}, with products defined as described above. If you have a strong math background, you may recognize this as the four-dimensional cyclic group, denoted \mathbb{Z}_4. In general, the cyclic groups \mathbb{Z}_n consist of a set of elements \{1, g, g^2, ..., g^{n-1}\}, with products defined in the obvious way that g^{j} g^{k} = g^{(j+k\ {\rm mod}\ n)}.
Thus far, this is just a transformation group; but, it will be a symmetry for any system that looks identical from all four points of view, such as a square.
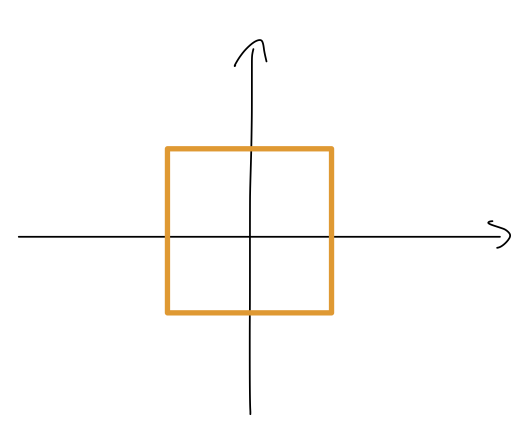
In fact, we could also describe this symmetry group as “the rotational symmetry group of a square”. (The full symmetry group of a square is the dihedral group D_4, which has 24 points of view that are generated by both rotations and reflections. But that would just complicate the math in this example without adding much else!)
9.3.1 Symmetry and representations
In physics especially, we’re not just interested in the structure of groups themselves; most of the groups we care about are symmetry groups, which means they also have an action associated with them, i.e. symmetry group elements act on physical objects and transform them in some way. In the example of discrete rotations above, group theory tells us how we can move our point of view of the system around, but to decide whether the system itself is invariant (looks the same), we need to know how the system itself responds to moving around the symmetry group.
A natural way to describe this aspect of symmetry in physics is with representation theory. Representation theory starts with a familiar but very big and flexible group called GL(N,\mathbb{C}), which is the group of N \times N invertible matrices with complex entries, under multiplication. (Actually, representation theory is more general than this - we could use real matrices, for example - but for quantum mechanics complex matrices are the most natural thing to use.) The idea is basically that matrices in GL(N,\mathbb{C}) are so flexible that if we are handed a group, we can completely mock up (or “represent”) the elements of the group and their products in terms of matrices with standard matrix multiplication.
Let’s be more concrete: a representation r is a map from a group G into matrices over a vector space V, r: G \rightarrow GL(V). Because this map is supposed to “represent” what the group does, it must “preserve the group product”: in other words, a \cdot b = c \Rightarrow r(a) r(b) = r(c) where the product between representations is defined by matrix multiplication. Now, this condition alone doesn’t give us the full structure of the group in our matrices: the simplest map we can always define is the trivial representation, r(g) = 1 for all g; this always satisfies the relationship r(a) r(b) = r(c), but it does so in sort of a simple way, by “collapsing” the whole group down to just the identity element. We can preserve the group structure through the map by insisting on a faithful representation, for which if a and b are distinct elements of the group G, we have r(a) \neq r(b).
Even with faithful representations, there can still be many ways to construct a representation r. Even for the simple cyclic group \mathbb{Z}_2, i.e. the group with two elements \{1, a\} and a^2 = 1, we can obtain a faithful representation of any dimension N just by mapping 1 into the N \times N identity matrix, and a into any N \times N matrix A = r(a) satisfying A^2 = 1 - of which there are an infinite number of possibilities! (The value N is said to be the dimension of the representation d_r.)
Having an infinite number of ways to map things seems bleak, but there are some very powerful results in representation theory that can simplify things. In particular, for a finite group G it can be proved that there are a finite number of unique “irreducible” representations, and any representation can be broken up into a combination of the irreducible ones. (In terms of our \mathbb{Z}_2 matrix example, most of the infinite set of matrices that square to 1 can be mapped into each other by a change of basis, and in the remaining classes we can identify subspaces of the matrices that repeat over and over.)
The mathematics of representation theory is beautiful and very deep, but we won’t go too far into it for this course, mostly just drawing on results as needed. (If you’re interested in a guided tour of more of the mathematics from a physics-friendly perspective, see this nice set of notes from a grad student at Harvard. ) But I want to elaborate on why representation theory is so useful for symmetries in physics: it gives us a really natural and powerful way to talk about how symmetry acts on physical objects! The basic idea is as follows:
- We write our symmetry down as a group.
- We classify every object in our system by its representation under the given symmetry group.
- Based on the two steps above, we know how everything transforms when we apply our symmetry, and we can identify whether things are invariant or not.
In step 2, specifying the representation includes the dimension d_R, which tells us that we have to describe our physical object as a vector of the same dimension. Symmetry operations are then matrices that act on these physical vectors. In quantum mechanics, this is obviously very natural: all of our quantum states are already complex vectors, and we already think of our symmetry operators \hat{U} as (unitary) matrices that act on our vectors.
You are, in fact, much more familiar with all of this than you might expect, although it probably wasn’t described in terms of groups and representations at first! A great example is rotational symmetry in classical mechanics. You already know that you can describe an arbitrary rotation in space in terms of 3x3 rotation matrices; these matrices form a group known as the “special orthogonal” group SO(3), which is the group of 3x3 matrices with \det R = 1 (special) and R^T R = 1 (orthogonal).
As you already know, rotation acts differently on different physical objects. Remembering back to classical mechanics, a position vector transforms differently from, say, the inertia tensor, which transforms differently from a scalar quantity like energy: \vec{r} \rightarrow R \vec{r} \\ I \rightarrow R^T I R \\ E \rightarrow E
Now that we know the mathematical language, it should be obvious that we can identify each of these quantities with a different representation of the rotation group! Specifically, energy lives in the trivial representation (doesn’t transform at all!), \vec{r} lives in a 3-dimensional representation (which turns out to be the d_r = 3 representation for SO(3),) and the inertia tensor I lives in a 9-dimensional representation. We’re still using 3x3 matrices to transform the inertia tensor, but this is just notation - I is a nine-component object, and we could rewrite it as a length-9 vector with a corresponding 9x9 rotation matrix.
Here, you should complete Tutorial 5 on “Symmetry groups and representations”. (Tutorials are not included with these lecture notes; if you’re in the class, you will find them on Canvas.)
When we discussed the parity operator \hat{P}, it was in the context of wave mechanics, which uses the infinite-dimensional Hilbert space spanned by \ket{x}. Parity acts to map us to the state on the opposite side of the origin, \hat{P} \ket{x} = \ket{-x}. With infinite dimensions we can’t really use matrices for our operators, but we can sort of think of this schematically as a matrix: if we consider the states near the origin, say \{...\ket{-2\epsilon}, \ket{-\epsilon}, \ket{0}, \ket{\epsilon}, \ket{2\epsilon}, ...\}, then the matrix elements locally look like this: \hat{P} = \left(\begin{array}{ccccc} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \end{array}\right) with the matrix extending infinitely in both directions. This is an infinite-dimensional representation for the parity symmetry group, \mathbb{Z}_2; even though the matrix is infinite, it should be intuitive that squaring it will give the identity.
Let’s consider some other representations of the same symmetry. Consider an H_2 molecule:
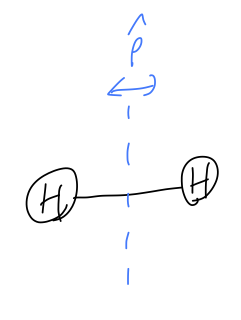
Label the two atoms as A and B, and the respective quantum states as \ket{A} and \ket{B} (which could represent, say, which atom an electron is localized around.) Then parity about the center of the molecule swaps \ket{A} with \ket{B}, so it is represented by the two-dimensional matrix \hat{P} = \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) which again is easily verified as a giving a representation of \mathbb{Z}_2. You can see the pattern here and write similar results for any number of dimensions in-between. Of course, part of the reason this is so simple is because the group \mathbb{Z}_2 is so tiny. More complicated groups will have more interesting and varied representations as we change the number of dimensions.
One more little fact about representations of \mathbb{Z}_2, i.e. parity. We know that given a quantum operator, we can (usually) compute its eigenvalues and eigenkets, and then it’s possible to change to a basis in which this is diagonal. We can certainly do this for the H2 example above; the matrix is just the Pauli matrix \hat{\sigma}_x, and its eigenvalues are \pm 1. So after a basis change, we can rewrite it as \hat{P} \rightarrow \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right) and the eigenvectors are \ket{+} = (1, 1), the parity-even superposition of the two atoms, and \ket{-} = (1, -1), the parity-odd superposition. In fact, this is a very general fact about representations over the complex numbers for \mathbb{Z}_2: there are only two irreducible representations (“irreps”), the “trivial” representation and the “sign” representation, both of which are one-dimensional: T:\ r(1) = 1, r(p) = 1; \\ S:\ r(1) = 1, r(p) = -1. If we start with a \hat{P} operator in N dimensions, it can always be diagonalized and reduced to a set of vectors which transform either according to the trivial irrep T (physically, these are “even states” under parity), or the sign irrep S (“odd states”).
9.4 Lattice translation symmetry
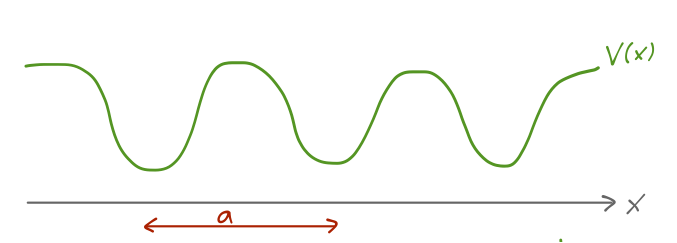
There is another, much more powerful example of a discrete symmetry that we can find in a potential V(x), which is known as periodicity: in one dimension, it is the condition that V(x \pm a) = V(x) for some particular length scale a. The corresponding symmetry transformation \hat{T} - shifting our potential by a finite length a - is known as finite translation or lattice translation (to distinguish it from symmetry under infinitesmal translations by some arbitrary \epsilon.) Obviously, this will be an extremely important symmetry for the description of crystals and other solid-state systems.
Let’s define explicitly the translation operator which will act on our system by performing a finite shift; we’ll call it \hat{\tau}(L), to distinguish it from the more general \hat{T} transformation, and we consider the case of an arbitrary shift by some length scale L. The action on position states is obvious: \hat{\tau}(L) \ket{x} = \ket{x+L}. This tells us that the position operator itself must transform as \hat{\tau}^\dagger(L) \hat{x} \hat{\tau}(L) = \hat{x} + L. Furthermore, we expect that translation by -L and then by L should give back the original state, from which we see that \hat{\tau}^{-1}(L) = \hat{\tau}(-L). However, we can see that \hat{\tau}^\dagger(-L) \hat{x} \hat{\tau}(-L) = \hat{x} - L \\ \hat{\tau}^\dagger(L) [...] \hat{\tau}(L) = \hat{\tau}^\dagger(L) \hat{x} \hat{\tau}(L) - L \hat{\tau}^\dagger(L) \hat{\tau}(L) \\ = \hat{x} + L (1 - \hat{\tau}^\dagger(L) \hat{\tau}(L)) which, given the observation that \hat{\tau}^{-1}(L) = \hat{\tau}(-L), must equal \hat{x}; so we also find that \hat{\tau}(L) is a unitary operator (which Wigner’s theorem told us anyway, but it’s always good to check!)
What about the momentum operator? \bra{x'} \hat{\tau}^\dagger(L) \hat{p} \hat{\tau}(L) \ket{x} = \bra{x'+L} \hat{p} \ket{x+L} = \delta((x+L) - (x'+L)) \frac{\hbar}{i} \frac{\partial}{\partial x} \\ = \delta(x - x') \frac{\hbar}{i} \frac{\partial}{\partial x} = \bra{x'} \hat{p} \ket{x} i.e. finite translation leaves the momentum unchanged (as we might have intuitively guessed.)
Once again, we should emphasize that for a system with lattice translation invariance, translation by an arbitrary length L will not be a symmetry. However, for the particular operator \tau(a) such that \hat{\tau}^\dagger(a) V(\hat{x}) \hat{\tau}(a) = V(\hat{x} + a) = V(\hat{x}) then we find that \hat{\tau}^\dagger(a) \hat{H} \hat{\tau}(a) = \hat{H} \\ \Rightarrow [\hat{H}, \hat{\tau}(a)] = 0. where the last line follows since \hat{\tau}(L) is unitary. This commutator guarantees that we will be able to find simultaneous eigenstates of \hat{H} and \hat{\tau}(a).
9.4.1 Tight-binding approximation
It’s interesting to start with the case of a potential which is periodic, but with infinite potential barriers between neighboring identical wells of width a.
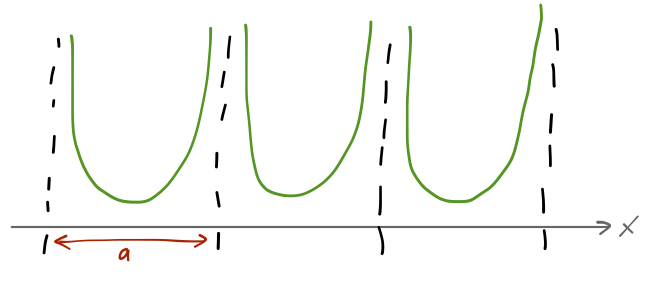
Suppose that if we solved the Schrödinger equation for one copy of this potential, we would find a set of bound states with energies E. Labeling the infinite set of wells by some integers n, we can construct a state \ket{n, E} which is equal to the E eigenstate in well n, and zero elsewhere. So \hat{H} \ket{n, E} = E \ket{n, E}, and there are an infinite number of such states in our infinite, periodic potential.
These states, however, are not eigenstates of the lattice translation operator, which clearly acts to give us \hat{\tau}(a) \ket{n, E} = \ket{n+1, E}. This should remind you a little bit of a ladder operator, and of coherent states in the simple harmonic oscillator, since it should be obvious that if we want to find an eigenstate of \hat{\tau}(a) it’s going to have to be in the form of an infinite sum. Let’s try a state of the following form: \ket{\theta, E} = \sum_{n=-\infty}^\infty e^{in\theta} \ket{n,E}. Acting with the translation operator, we see that \hat{\tau}(a) \ket{\theta, E} = \sum_{n=-\infty}^\infty e^{in \theta} \ket{n+1, E} \\ = \sum_{n=-\infty}^\infty e^{i(n-1)\theta} \ket{n, E} \\ = e^{-i\theta} \ket{\theta, E}. So indeed, \ket{\theta, E} is an eigenstate of lattice translation (and also of \hat{H}, since we constructed it as a sum of energy eigenstates.) The eigenvalue with respect to translation is a pure phase, so we can see that \ket{\theta, E} = \ket{\theta+2\pi, E} for any \theta. By convention we take the physical state to be labelled by -\pi < \theta \leq \pi.
Although the above derivation works just fine, the first step is a little vague. A reasonable question to ask is, why should the coefficients of \ket{\theta, E} be pure phases, instead of just arbitrary complex numbers?
The best way to answer this question is to just try the more general expansion: we allow an arbitrary complex coefficient for each well eigenstate,
\ket{T, E} = \sum_{n=-\infty}^\infty z_n \ket{n, E}.
Now what happens if we act with the translation operator? We find the following, doing the same sum redefinition trick: \hat{\tau}(a) \ket{T, E} = \sum_{n=-\infty}^\infty z_{n-1} \ket{n, E}. In general, there’s no reason for this state to be a translation eigenstate. But if we assume it is, then we find the equation \hat{\tau}(a) \ket{T, E} = T \ket{T, E} \\ \sum_{n=-\infty}^\infty z_{n-1} \ket{n,E} = T \sum_{n=-\infty}^\infty z_n \ket{n,E}. Since both sides are summing over the same states, every coefficient in the sum has to be identical, i.e. we find the result z_{n-1} = T z_n. This is a significant constraint, but it doesn’t prove the z_n must be a phase yet. We go a step further and apply the identity operator, in the form \hat{\tau}^\dagger(a) \hat{\tau}(a): \bra{T, E} \hat{\tau}^\dagger(a) \hat{\tau}(a) \ket{T,E} = |T|^2 since \bra{T,E} \hat{\tau}^\dagger(a) = (\hat{\tau}(a) \ket{T,E})^\dagger. But this is also just \left\langle T,E | T,E \right\rangle = 1, so T must be a pure phase T = e^{i\theta}, which means that z_n = e^{in\theta} z_0. So up to an overall constant, the form \ket{\theta, E} is the only possibility for an eigenstate of \hat{\tau}(a). The key here is actually a much more general result, which we basically just proved: the eigenvalues of a unitary operator are pure phases.
This is a good point to briefly connect back to our discussion about groups and representations. If we had a potential that was invariant under translation and was also finite, e.g. there was a periodic boundary somewhere (like a ring of N atoms), then we would have \tau(a)^N = 1, and the symmetry corresponding to translation would be the cyclic group \mathbb{Z}_N. However, we’ve been considering the case of infinite potentials here, which we can think of as the limit of \mathbb{Z}_N with N \rightarrow \infty; this just gives us back \mathbb{Z}, the group formed by the integers under addition. Since \mathbb{Z} is infinite, a faithful representation in terms of our original basis \ket{n, E} takes the form of an infinite-dimensional matrix.
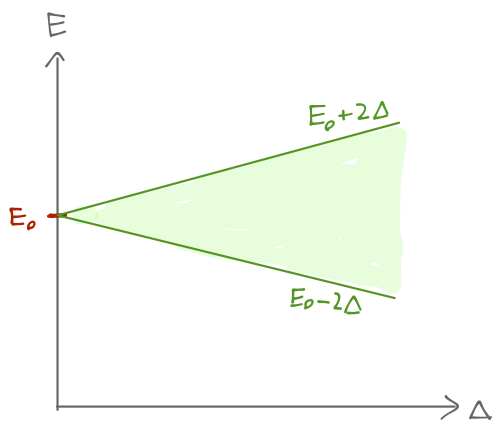
This is, so far, something of a formal exercise; the construction of the \ket{\theta, E} states doesn’t alter the energy spectrum at all since the wells have infinite barriers between them. At this point we’ll focus on a single eigenstate E_0, and label our well-centered states as \ket{n}. Let’s lower the barriers between the wells to be finite, but still high. In fact, we will assume that the barriers are high enough that while tunneling between adjacent wells is possible, leading to overlap of the wavefunctions, the overlap with wells separated by two or more barriers is totally negligible. In other words, the matrix elements of the Hamiltonian between localized states is \bra{n} \hat{H} \ket{n} = E_0 \\ \bra{n'} \hat{H} \ket{n} = -\Delta \delta_{n', n\pm 1}. This set of assumptions is known in solid state physics as the tight-binding approximation. Now, the localized states in an individual well are no longer energy eigenstates: the action of the Hamiltonian gives us \hat{H} \ket{n} = E_0 \ket{n} - \Delta \ket{n+1} - \Delta \ket{n-1}. However, it turns out that the \ket{\theta} translation eigenstates are still energy eigenstates! \hat{H} \ket{\theta} = E_0 \ket{\theta} - \Delta \sum_{n=-\infty}^\infty \left( e^{in\theta} \ket{n+1} + e^{in\theta} \ket{n-1} \right) \\ = E_0 \ket{\theta} - \Delta (e^{-i\theta} + e^{i\theta}) \ket{\theta} \\ = (E_0 - 2\Delta \cos \theta) \ket{\theta}. So as a result of the interaction term \Delta, our single, discrete bound-state energy has split into a continuous band of energies in the range E \in [E_0 - 2\Delta, E_0 + 2\Delta].
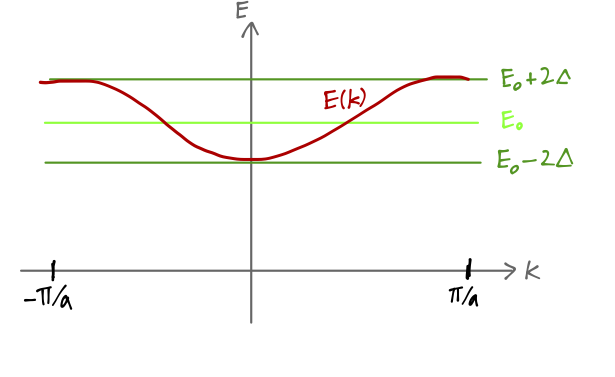
The wavefunctions corresponding to these continuous energies should also look different, now that tunneling between wells is allowed. We know that for any particular choice of \theta, the position-space wavefunction will be \left\langle x | \theta \right\rangle. But now we notice that \bra{x} \hat{\tau}(a) \ket{\theta} = \left\langle x-a | \theta \right\rangle \\ = \left\langle x | \theta \right\rangle e^{-i\theta} letting \hat{\tau}(a) act to the left and then to the right. For these two quantities to be equal, the wavefunction must be (1) periodic under lattice translation, except for (2) a part which kicks out exactly e^{-i\theta} when we shift x \rightarrow x-a. In other words, the wavefunction must take the form \left\langle x | \theta \right\rangle = e^{i\theta x/a} u_k(x), where u_k(x) is a periodic function with the same period as V(x), i.e. u_k(x+a) = u_k(x). The other piece here is a plane wave, from which we read off the wave number k = \theta/a. The observation above, that the wavefunction in the presence of a translation symmetry splits into a plane wave times a periodic function, is known as Bloch’s theorem; the periodic functions themselves are called Bloch functions. Preferring to work with the wave number, we see that the physical states are now labelled by -\pi/a < k \leq \pi/a, and the corresponding bound-state energies are E(k) = E_0 - 2\Delta \cos ka
This range of allowed distinct values for k (or equivalently the range E_0 - 2 \Delta \leq E \leq E_0 + 2\Delta) is known as the Brillouin zone associated with this potential.
It’s worth noting that the fact that we obtain a continuous band of energies E(k) is entirely because we have assumed that our potential is built from an infinite number of distinct, localized wells. We could have instead a finite chain of length N, say with periodic boundary conditions so that translation from well N returns us back to well 1. Then we must have \bra{x} \hat{t}(a)^N \ket{\theta} = \left\langle x | \theta \right\rangle = \left\langle x-Na | \theta \right\rangle = \left\langle x | \theta \right\rangle e^{iN\theta} which gives us a quantization condition, \theta = \frac{2\pi}{N} j where j is an integer between (-N/2, N/2). So with a finite number of states to translate between, we return to the case of having a discrete number of energy levels.
Let’s go back and focus more on the relationship between energy and wave number that we found above for the case when \ket{\theta} is also an energy eigenstate: E(k) = E_0 - 2\Delta \cos ka.
An equation of this form relating energy and wave number/momentum is known as a dispersion relation. What does this equation really mean, and why is it called a “dispersion relation”? The short answer is that the relationship between energy and wave number is crucial in how quantum states evolve in time and space. Recall that for a plane wave solution, the time-dependent wavefunction is u_E(x,t) = Ae^{i(kx-\omega t)} + Be^{-i(kx+\omega t)} where \omega = E/\hbar. A dispersion relation generalizes this form to systems where E(k) is different than the simple E \sim k^2 relationship for free particles. The exact form of the dispersion relation literally controls the dispersal of initial quantum states. (For example, a wave packet built of free plane waves will spread out in time. For a particle with linear dispersion, i.e. a photon \omega = ck, then there is no dispersal; the shape of a wave packet would be fixed as time evolves.)
9.5 Example: periodic delta functions
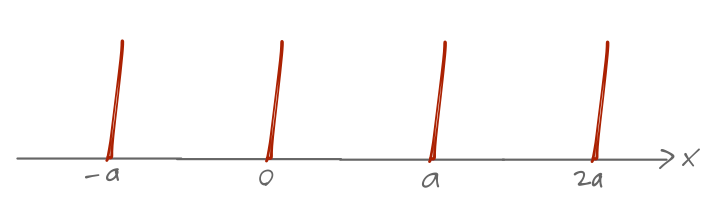
Let’s go back to periodic symmetry and try an explicit example with a simple model: a periodic array of identical delta functions, V(x) = \sum_{n=-\infty}^\infty V_0 \delta(x-na) where I’m assuming V_0 > 0.
From our derivation before, we know that a general energy eigenstate can be written as a Bloch function times a plane wave, \psi(x) = e^{ikx} u_k(x) where u_k(x+a) = u_k(x). We also know that the full wavefunction between the delta functions must look like the sum of plane waves alone, \psi(x) = A e^{iqx} + B e^{-iqx}, where E(q) = \hbar^2 q^2 / (2m). Comparing the two equations, we see that the Bloch function has to be u_k(x) = A e^{i(q-k)x} + B e^{-i(q+k)x}. Now we apply the boundary conditions. Since u_k(0) = u_k(a), we see that A + B = A e^{i(q-k)a} + B e^{-i(q+k)a}. The other boundary condition, which you’re now quite familiar with from the homework, is that the derivative \psi'(x) will have a specific discontinuity due to the delta functions: \psi'(\epsilon) - \psi'(-\epsilon) = \frac{2mV_0}{\hbar^2} \psi(0) = \frac{2mV_0}{\hbar^2} (A+B). Exploiting the periodicity of the wavefunction, we can write \psi'(-\epsilon) = \psi'(a-\epsilon) e^{-ika}. Combining, we find the boundary condition \frac{2mV_0}{\hbar^2} (A+B) = iq[A (1-e^{i(q-k)a}) - B (1-e^{-i(q+k)a})]. Solving the two boundary conditions gives us a transcendental equation relating k and q: \cos (ka) = \cos (qa) + \frac{mV_0a}{\hbar^2} \frac{\sin(qa)}{qa}. (As a quick check on units: \hbar^2 has units of energy times time squared, [E]^2 [t]^2, which is [m]^2 [d]^2 / [t]^2. Dividing by ma leaves units of [m] [d] / [t]^2, mass times acceleration, which is energy - cancelling the V_0 so that the combination is dimensionless as it must be.)
Derive the equation above relating k to q, using the boundary condition equations we found above.
Answer:
Solving for continuity first, we can obtain the ratio B/A: 1 + \frac{B}{A} = e^{i(q-k)a} + \frac{B}{A} e^{-i(q+k)a} \\ \frac{B}{A} \left(1 - e^{-i(q+k)a} \right) = e^{i(q-k)a} - 1 \\ \frac{B}{A} = \frac{e^{i(q-k)a} - 1}{1 - e^{-i(q+k)a}}.
Now we plug this in to the other boundary equation: \frac{2mV_0}{\hbar^2} \left(1 + \frac{B}{A} \right) = iq [(1 - e^{i(q-k)a}) - \frac{B}{A} (1 - e^{-i(q+k)a})] \\ \frac{2mV_0}{\hbar^2} \frac{e^{i(q-k)a} - e^{-i(q+k)a}}{1 - e^{-i(q+k)a}} = iq[ (1 - e^{i(q-k)a}) - (e^{i(q-k)a} - 1)] \\ = 2iq(e^{i(q-k)a} - 1). This looks messy still, but let’s clear out the denominator on the left and try to simplify: \frac{mV_0}{\hbar^2} \left( e^{i(q-k)a} - e^{-i(q+k)a} \right) = iq(e^{i(q-k)a} - 1)(1 - e^{-i(q+k)a}) \\ \frac{mV_0}{\hbar^2} e^{-ika} (e^{iqa} - e^{-iqa}) = iq (e^{i(q-k)a} + e^{-i(q+k)a} - e^{-2ika} - 1) \\ \frac{mV_0}{\hbar^2} (2i \sin (qa)) = iq (e^{iqa} + e^{-iqa} - e^{-ika} - e^{+ika}) \\ = iq (2 \cos (qa) - 2 \cos(ka)) or cancelling off the 2i and rearranging, \cos(ka) = \cos(qa) + \frac{mV_0}{\hbar^2} \frac{\sin (qa)}{q} reproducing the result above.
Now we recall that q determines the energy of our state, E = \hbar^2 q^2 / 2m. In the limit q \rightarrow \infty, we just have \cos (ka) = \cos (qa), and we recover the standard free-particle dispersion E(k) = \hbar^2 k^2 / 2m. However, for smaller values of qa, the right-hand side of this equation can be larger than 1 (or smaller than -1), whereas the left-hand side can’t be.
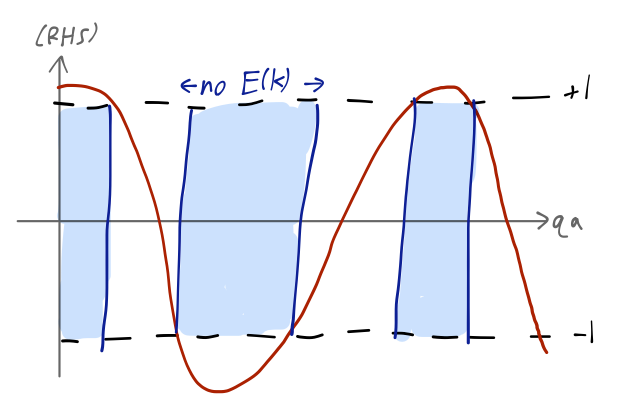
So certain values of E (and thus q) can never satisfy this equation. When the right-hand side of this equation is between -1 and 1, we find a continuum E(k) of possible energies, known as a band. The forbidden regions between the bands are known as band gaps.
Some bands have much larger separations in energy than others. If you imagine the bands as being filled with single electrons, you can begin to see the difference between a metal (in which it’s easy to excite an electron out of the ground state), and an insulator (in which it isn’t easy.)
9.6 Continuous symmetries
We’ve seen now a few example of symmetries, i.e. operations under which a particular physical system is invariant. We’ve constructed explicit operators corresponding to these symmetries, and so far the operators have always been unitary (thanks to Wigner’s theorem.)
It is a general fact that if we have a Hermitian operator \hat{Q}, then we can construct a unitary operator by exponentiating it: \hat{U}(a) = \exp \left( -\frac{i \hat{Q} a}{\hbar} \right) (The sign and the presence of \hbar are by convention.) It should be clear that for Hermitian \hat{Q}, we have \hat{U}{}^\dagger \hat{U} = 1. In fact, what we’ve constructed here is a whole family of unitary operators, parameterized by the arbitrary constant a. The Hermitian operator \hat{Q} inside the exponent is called the generator of this family of unitary symmetry operators. We’ve seen an example of this construction before: the unitary time-translation operator, e^{-i\hat{H} t/\hbar}.
In fact, we’ve just seen another example of a one-parameter family of symmetry operators: the translation operator \hat{\tau}(L). Can we write this in terms of another operator which is a Hermitian generator? To answer that question, it’s useful to study what happens when the translation becomes very small: \bra{x} \hat{\tau}(\epsilon) \ket{\psi} = \psi(x-\epsilon). We know that \epsilon = 0 corresponds to no translation at all, i.e. \hat{\tau}(0) = 1. Therefore, in the limit of small \epsilon we must be able to rewrite \hat{\tau}(\epsilon) by series expanding the exponential to find \hat{\tau}(\epsilon) = 1 - \frac{i\epsilon}{\hbar} \hat{G} + ... for some Hermitian generator \hat{G}. Expanding both sides of the above equation then gives us \left\langle x | \psi \right\rangle - \frac{i\epsilon}{\hbar} \bra{x} \hat{G} \ket{\psi} = \psi(x) - \epsilon \frac{d\psi}{dx}. So for spatial translations, \hat{G} is just the momentum operator, \hat{p}. Although we’ve only shown that momentum gives rise to infinitesmal translations, we can “build up” a finite translation operator as a series of many infinitesmal ones and this just gives us back the same exponential form, either directly from an infinite product: \hat{\tau}(a) = \lim_{N \rightarrow \infty} \left(1 - \frac{i \hat{p}}{\hbar} \frac{a}{N} \right)^N = \exp \left( -\frac{i \hat{p} a}{\hbar}\right), or just by writing the infinitesmal form as an exponential, and then \hat{\tau}(a) = \hat{\tau}(\epsilon)^N = \exp \left( \frac{-i \hat{p} \epsilon}{\hbar} \right)^N = \exp \left( \frac{-i \hat{p} (N \epsilon)}{\hbar} \right) \rightarrow \exp \left( \frac{-i\hat{p} a}{\hbar} \right).
So we know two generators the Hamiltonian is the generator of time translations, and the momentum operator is the generator of spatial translations.
This is an example of a continuous symmetry, since it depends on a continuous parameter, the translation distance. This is as opposed to the discrete symmetries we’ve seen, which cannot be decomposed in this way. As the name implies, discrete symmetries generally have a discrete (i.e. finite) set of eigenvalues and eigenvectors; parity has just two. Lattice translation on a ring of N atoms has N eigenvalues. (Lattice translation on an infinite chain is sort of an edge case; you can think of it as an infinite limit of a finite symmetry.)
As we already saw, for any symmetry, we may find that in addition to the states of our Hilbert space, some operators are left invariant as well, i.e. \bra{\psi} \hat{U}{}^\dagger \hat{A} \hat{U} \ket{\psi} = \bra{\psi} \hat{A} \ket{\psi}. Since \hat{U} is unitary, this is equivalent to the condition [\hat{A}, \hat{U}] = 0. Moreover, if \hat{U} is continuous, then we can write \hat{U} = 1 - i \hat{Q} (\Delta a) / \hbar + ..., and so this immediately implies that [\hat{A}, \hat{Q}] = 0. For symmetries of the Hamiltonian, this has a particularly important consequence; we find that if [\hat{H}, \hat{U}] = 0 and \hat{U} is a continuous symmetry generated by \hat{Q}, then [\hat{H}, \hat{Q}] = 0. This is really easy to derive, but important enough to put in a box:
If a continuous symmetry \hat{U} is a dynamical symmetry, i.e. if [\hat{U}, \hat{H}] = 0, then the corresponding generator \hat{Q} of \hat{U} is a conserved quantity, i.e. [\hat{U}, \hat{H}] = 0 \Rightarrow \frac{d\hat{Q}}{dt} = 0.
In classical mechanics, Noether’s theorem (symmetries lead to conserved quantities) should be familiar to you already; the quantum version is much simpler to derive, but no less powerful. So, from the examples we’ve seen, invariance of a physical system under translations in space and time lead to conservation of momentum and energy, respectively.
It is a fact that all known fundamental interactions do conserve energy and momentum; so as long as we take all of the interactions into account (so that we have no “external” sources or potentials), we will find that infinitesmal translation in time and space is always a symmetry.
The exponential map that we use to write a unitary symmetry operator in terms of a Hermitian generator immediately implies some useful properties. If \hat{C}_a is a continuous symmetry operator with parameter a \in \mathbb{R}, and it is generated by \hat{C}_a = \exp \left( -\frac{i\hat{G} a}{\hbar} \right), then it satisfies the following properties:
Composition: \hat{C}_a \hat{C}_b = \hat{C}_{a+b}
Identity transformation: \hat{C}_0 = \hat{1}
Inverse + unitarity: \hat{C}_a^{-1} = \hat{C}_a^{\dagger} = \hat{C}_{-a}.
The last two properties tell us immediately that for infinitesmal parameter value \epsilon, \hat{C}_\epsilon = \hat{1} - i\epsilon \hat{G} / \hbar for Hermitian generator \hat{G}, so that \hat{C}_\epsilon \hat{C}_{-\epsilon} = \hat{1}
at first order in \epsilon. We can then derive the exponential map for arbitrary a, by repeatedly applying infinitesmal transformations or by using composition to derive a differential equation. (See Merzbacher 4.6.)
You will recognize these properties: they are exactly the properties of a group! Specifically, these relations (together with the exponential map from Hermitian generator to unitary operator) define an object known as a Lie group. Lie groups are infinite, and they are smoothly connected to the identity, meaning that infinitesmal transformations are well-defined (which, in turn, lets us naturally work with familiar tools like derivatives and power series.) The group GL(N,\mathbb{C}) that appeared in our definition of represenations is itself a Lie group.
The mathematics of Lie groups is deep and beautiful, but we won’t dive into the general story in this class, we’ll borrow important math results as we need them. As far as I know, all continuous symmetry groups in physics are Lie groups. Some of them have multiple parameters, like rotations in three dimensions, as we will see.
One final thing that is interesting to point out with our new formalism is that the connection between position and momentum through a symmetry operator gives us another way to understand the canonical commutation relation. Let’s consider a translation by an infinitesmal distance \epsilon: \hat{U}(\epsilon) \ket{x} = \ket{x+\epsilon} Now, if we apply \hat{x} to both sides, it should produce a factor of (x + \epsilon), since it’s the same state on both sides. But we can also calculate the commutator of \hat{x} with the translation operator: [\hat{x}, \hat{U}(\epsilon)] = [\hat{x}, \left(1 - \frac{i\hat{p} \epsilon}{\hbar} \right)] \\ = -\frac{i\epsilon}{\hbar} [\hat{x}, \hat{p}]. So this tells us that \hat{x} \hat{U}(\epsilon) \ket{x} = \hat{U}(\epsilon) \hat{x} \ket{x} + [\hat{x}, \hat{U}(\epsilon)] \ket{x} \\ (x+\epsilon) \ket{x+\epsilon} = x \ket{x + \epsilon} - \frac{i\epsilon}{\hbar} [\hat{x}, \hat{p}] \ket{x} \\ We can cancel off the x \ket{x+\epsilon} from both sides, and then notice that to leading order in \epsilon, \epsilon \ket{x+\epsilon} \approx \epsilon \ket{x}. Then comparing what we have left, we can see that for any state \ket{x}, \epsilon = -\frac{i\epsilon}{\hbar} [\hat{x}, \hat{p}] \\ \Rightarrow [\hat{x}, \hat{p}] = i\hbar. So now we don’t have to take the relation as a postulate; it’s something we can derive from the fact that momentum is the generator of translations!
One last word on groups and representations. What is the symmetry group corresponding to translations? Well, since we can translate by any real number, it should be easy to convince yourself that translation is described by the group \mathbb{R}, the real numbers. \mathbb{R} is a Lie group, an especially simple one since all operations commute (we can apply two translations in either order and the result is the same.)
As for the representations, recall that for parity \hat{P}, we could decompose N-dimensional parity representations into one-dimensional representations (vectors) that were either even or odd under parity. Here, the mathematical result is similar; \mathbb{R} can be completely reduced to one-dimensional representations. Unlike parity, here there are an infinite number of such representations, and they are labelled by the momentum eigenvalue p (since each \ket{p} will transform slightly differently under \hat{U}(L).) In other words, the (irreducible) representations of translation symmetry are simply the momentum eigenvectors \ket{p}; to know how an arbitrary physical state transforms under translation, we just expand in momentum states (or position states, since we know that’s just a change of basis.)