25 Propagators and path integration
As far as time evolution in quantum mechanics goes, we’ve seen a fair amount of formalism by now, but a lot of it has focused on evolution of quantum states. While this is technically all that we need to study any quantum system, it will be useful to focus a bit more specifically on time evolution for particles propagating in space. This will lead us to some very useful tools: the propagator, and the path integral.
25.1 Propagation of plane waves and wave packets
Let’s begin by reminding ourselves of how time evolution works for simple, free solutions in quantum mechanics: that is, solutions where the potential is V(\hat{x}) = 0, so the Hamiltonian is \hat{H} = \hat{p}^2 / 2m. Our energy eigenstate solutions, which are also momentum eigenstates, are plane waves: \psi_E(x) = Ae^{ikx} + Be^{-ikx} where the wave number k = p/\hbar. Acting with the time evolution operator gives us an overall phase since this is an energy eigenstate, \psi_E(x,t) = \bra{x} \exp \left( \frac{-i \hat{H} t}{\hbar} \right) \ket{\psi} = e^{-iEt/\hbar} \left\langle x | \psi \right\rangle \\ = A e^{i(kx-\omega t)} + Be^{-i(kx+\omega t)}, with \omega = E/\hbar. Overall, each plane wave is represented as a pure phase, e^{i\phi(x,t)}. Moreover, we see that the value of the phase repeats in time, e.g. for wave A: kx = k\left(x+\frac{\omega}{k} t \right) - \omega t \\ \Rightarrow \phi_A(x,0) = \phi_A(x+\frac{\omega}{k} t,t). We identify v_p \equiv \omega / k as the phase velocity associated with our (right-moving) plane wave, A. Similarly, wave B moves to the left with the same phase velocity.

As implied by thinking about “right-moving” versus “left-moving”, a plane wave clearly represents a moving particle, in some way. This seems to match nicely onto the descriptions of the two plane-wave solutions as momentum eigenstates: acting with \hat{p} = -i\hbar \partial / \partial x we easily see that e^{ikx} is a momentum eigenstate with p = \hbar k, and similarly p = -\hbar k for the left-moving wave.
However, we notice something odd if we plug in the dispersion relation (energy-momentum relation) for a free particle to find the phase velocity: E(k) = \frac{\hbar^2 k^2}{2m} = \hbar \omega \\ \Rightarrow v_p = \frac{\omega}{k} = \frac{\hbar k}{2m} = \frac{p}{2m}. This is only half of the classical momentum of a single particle! Why is there a discrepancy?
We have to remember that a plane wave is something of an odd object. For simplicity I will set B=0 and focus on a right-moving plane wave. If we’re going to try to do an experiment to find out the velocity of our particle, we have to measure its position at successive times: Born’s rule tells us that the probability of any outcome is p(x) = \int_{-\infty}^\infty dx' \delta(x-x') |\psi(x',t)|^2 = |\psi(x,t)|^2. But for a plane wave, |\psi(x,t)|^2 is a constant, A^2! So we’re equally likely to find our particle anywhere, at any t, regardless of the phase velocity. Thus we shouldn’t be worried that the phase velocity doesn’t equal the classical velocity, because the phase velocity clearly doesn’t have the same physical meaning. (I am not aware of any good explanation of why it should be precisely half of the classical velocity, but at least the fact that it is different from the classical velocity shouldn’t bother us.)
To make a proper comparison with the classical velocity of a particle, we have to start with a more localized state; a natural candidate is the wave packet, which we met before as a minimum-uncertainty solution to the free Hamiltonian. Given the parameters x_0, k_0, and \Delta x, the wave packet solution is \psi(x,0) \propto \exp \left( ik_0 x - \frac{(x-x_0)^2}{4(\Delta x)^2} \right) As we’ve seen before, this looks like plane wave multiplied by a Gaussian “envelope”; the probability density |\psi(x,0)|^2 is pure Gaussian, centered at x_0 and with width (\Delta x). If we take the Fourier transform of a Gaussian, we find another Gaussian in momentum space: \tilde{\psi}(k,0) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty dx\ \psi(x,0) e^{-ikx} \\ \propto \exp \left[ -ik x_0 - \frac{(k-k_0)^2}{4(\Delta k)^2} \right]. where \Delta k = 1 / (2 \Delta x). Now, calculating the time evolution of this state requires a bit more work, since it’s a linear combination of many momentum states. However, since we are considering a free particle (the potential V(x) is constant), we can observe that [\hat{H}, \hat{p}] = 0, so the momentum eigenstates are also energy eigenstates. This means that the time-evolution in momentum space is very simple: \psi(k,t) = \left\langle k | \psi(t) \right\rangle = \bra{k} e^{i\hat{H} t/\hbar} \ket{\psi(0)} = e^{i\omega(k) t} \tilde{\psi}(k,0) where \omega(k) = E(k)/\hbar for a free particle.
Fourier transforming back to position space, the time-evolved wave packet is thus \psi(x,t) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty dk\ \exp \left[ -ikx_0 - \frac{(k-k_0)^2}{4(\Delta k)^2} \right] e^{i \phi(k)} where I’ve defined the phase \phi(k) = kx - \omega(k) t. Note that this equation holds for wave packets in any quantum system in which the momentum is continuous and uniquely specifies the energy through a dispersion relation \omega(k). Although we started with the free wave packet, let’s try to be a little more general now. Since our wave packet is sharply peaked around k=k_0, let’s try to do a Taylor expansion of the phase \phi(k) about the same point: \phi(k) \approx \phi_0 + \phi'_0 (k-k_0) + \frac{1}{2} \phi''_0 (k-k_0)^2 where \phi_0 = k_0 x - \omega_0 t \\ \phi'_0 = \left. \frac{d\phi}{dk} \right|_{k=k_0} = x - \frac{d\omega}{dk} t \\ \equiv x - v_g t \\ \phi''_0 = \left. \frac{d^2 \phi}{dk^2} \right|_{k=k_0} = -\frac{d^2 \omega}{dk^2} t \\ \equiv -\alpha t Plugging back in, we find \psi(x,t) \propto e^{i (k_0 x - \omega_0 t)} \int_{-\infty}^\infty dk\ \exp \left[ i(k-k_0) \left( x-x_0 - v_g t\right) - (k-k_0)^2 \left( \frac{1}{4(\Delta k)^2} + i \alpha t) \right) \right].
You’ll recognize this as a Gaussian integral; with some appropriate changes of variables we can reduce the integrand to something of the form e^{-u^2} and then do it. I’ll just tell you the result, up to normalizing constants that I’ve been ignoring anyway: \psi(x,t) \propto \exp \left[ i(k_0 x - \omega_0 t) - (x-x_0 - v_g t)^2 \frac{1 - 2\alpha i (\Delta k)^2 t }{4\sigma(t)^2} \right]. with \sigma^2(t) = (\Delta x)^2 + \frac{\alpha^2 t^2}{4 (\Delta x)^2}. At t=0 this reduces to our original formula for the wave packet, which is a good cross-check. This formula is a little intimidating, but if we square it to find the probability density for finding our particle at position x, it becomes illuminating: |\psi(x,t)|^2 \propto \frac{1}{\sigma(t)} \exp \left[ -\frac{(x-x_0 - v_g t)^2}{2 \sigma^2(t)} \right]. This is, once again, a Gaussian distribution, but with the peak translated from x_0 to x_0 + v_g t. So the constant v_g = d\omega / dk is exactly what we should interpret as the analogue of the classical speed of our particle; it determines the rate at which the most likely outcome of measuring x changes. v_g is called the group velocity. It’s easy to check that the dispersion relation for a free particle gives us v_g = \frac{\hbar k}{m} = \frac{p}{m}, matching on to the classical expectation. So to summarize, the center of a wave packet travels at the group velocity v_g = d\omega / dk, while the phase of a plane wave changes with the phase velocity v_p = \omega / k. The wave packet is the closest analogue to a classical experiment involving a single particle; a plane wave is better thought of as a continuous stream of particles moving in one direction.
One other observation we can make from our result for the evolution of a wave packet is that although it remains Gaussian, the width of the packet \sigma(t) increases over time, according to the constant \alpha = d^2 \omega / dk^2, which is commonly called the “group velocity dispersion” or sometimes just “the dispersion”. Since \sigma(t) \sim \alpha^2, you can see that whatever the sign of \alpha, the wave packet will spread out over time; for example, for the free particle we have \alpha_{\rm free} = \frac{\hbar}{m}.
The only exception to the spreading of wave packets occurs when \alpha = 0. This is the case for systems with linear dispersion relations, \omega(k) = ck; light waves are one example. Linear dispersion also leads to the property that v_p = v_g, e.g. light waves and light pulses travel at the same speed, c.
25.2 Time evolution and propagators
Our method for finding the time evolution of the wave packet points us towards a more general procedure that we can use for time evolution of any wavefunction. We want to be as general as possible, so we don’t assume that momentum commutes with the Hamiltonian (it often doesn’t.) Instead, we just require that we can find some operator \hat{A} which satisfies [\hat{H}, \hat{A}] = 0. Then we can construct a set of simultaneous eigenvectors, i.e. to each eigenvector \ket{a} of \hat{A} we can assign a unique energy E_a. We can then calculate the time evolution of an arbitrary state by expanding in these eigenkets, \ket{\psi(t)} = \exp \left[ \frac{-i \hat{H} (t-t_0)}{\hbar} \right] \ket{\psi(t_0)} \\ = \sum_a \ket{a} \left\langle a | \psi(t_0) \right\rangle \exp \left[ \frac{-i E_a (t-t_0)}{\hbar} \right]. We can apply \bra{x} to both sides to see how the wavefunction in position space evolves: \left\langle \vec{x} | \psi(t) \right\rangle = \sum_a \left\langle \vec{x} | a \right\rangle \left\langle a | \psi(t_0) \right\rangle \exp \left[ \frac{-i E_a (t-t_0)}{\hbar} \right]. The second inner product here is exactly the expansion coefficients of the wavefunction for the \hat{A} eigenbasis: we can write \left\langle a | \psi(t_0) \right\rangle = \int d^3x' \left\langle a | \vec{x}' \right\rangle \left\langle \vec{x}' | \psi(t_0) \right\rangle. Combining these two expressions lets us rewrite the time-evolved wavefunction as an integral transformation from some initial time t_0, by inspection: \psi(\vec{x}',t) = \int d^3x K(\vec{x}',t; \vec{x}, t_0) \psi(\vec{x}, t_0) where the kernel function K is equal to K(\vec{x}', t; \vec{x}, t_0) = \sum_a \left\langle \vec{x}' | a \right\rangle \left\langle a | \vec{x} \right\rangle \exp \left[ \frac{-i E_a (t-t_0)}{\hbar} \right]. This kernel function K is called the propagator. Once we solve for the propagator for a particular operator \hat{A} which commutes with our Hamiltonian, then we can immediately write the time evolution of any wavefunction as an integral similarly.
This form reinforces the point that quantum mechanics is perfectly causal, despite the randomness; once we specify \psi(\vec{x}, t_0) and solve for the propagator, the wavefunction is totally determined for all time - as long as we don’t disturb the system, by making a measurement or in any other way.
Notice that the propagator can be written compactly as the matrix elements of the time-evolution operator in coordinate space: K(\vec{x}', t; \vec{x}, t_0) = \sum_a \left\langle \vec{x}' | a \right\rangle \exp \left[ \frac{-i E_a (t-t_0)}{\hbar} \right] \left\langle a | \vec{x} \right\rangle \\ = \bra{\vec{x}'} \exp \left[ \frac{-i \hat{H} (t-t_0)}{\hbar} \right] \ket{\vec{x}}. In the limit t \rightarrow t_0, the operator in the middle approaches the identity and we have simply \lim_{t \rightarrow t_0} K(\vec{x}', t; \vec{x}, t_0) = \delta^3 (\vec{x}' -\vec{x}). Physically, we can interpret the propagator itself as a function of \vec{x}' and t as the time-evolved wavefunction of a particle localized exactly at position \vec{x} at initial time t_0. In fact, treating the propagator as a wavefunction itself, it’s clear that it is a solution to the Schrödinger equation: \left[ - \frac{\hbar^2}{2m} (\nabla')^2 + V(\vec{x}') - i \hbar \frac{\partial}{\partial t} \right] K(\vec{x}', t; \vec{x}, t_0) = -i \hbar \delta^3 (\vec{x}' - \vec{x}) \delta(t-t_0), subject to the boundary condition K(\vec{x}', t; \vec{x}, t_0) = 0 for t < t_0, i.e. the solution is explicitly for times after t_0. Those of you familiar with integral solutions to differential equations, especially in electrostatics, will recognize the propagator K as nothing more than the Green’s function for the time-dependent Schrödinger equation.
Let’s go back to the case of the free particle in one dimension, \hat{H} = \hat{p}^2 / (2m). A good choice (really the only choice) for an observable commuting with \hat{H} is the momentum itself. This gives for the propagator K(x', t; x, t_0) = \bra{x'} e^{-i\hat{H} (t-t_0)/\hbar} \ket{x} \\ = \int dp \left\langle x' | p \right\rangle e^{-ip^2 (t-t_0)/2m\hbar} \left\langle p | x \right\rangle \\ = \frac{1}{2\pi \hbar} \int dp\ \exp \left[ \frac{ip (x'-x)}{\hbar} - \frac{ip^2 (t-t_0)}{2m\hbar} \right] \\ = \sqrt{\frac{m}{2\pi i \hbar (t-t_0)}} \exp \left[ \frac{im(x'-x)^2}{2\hbar (t-t_0)} \right] \Theta (t-t_0) where I’ve done the integral by completing the square to write it as a standard Gaussian, and I’ve added the Heaviside function to remind us that the propagator only applies for t > t_0. You can verify that if we set the initial state \psi(x,0) to be a wave packet, then using this propagator will allow us to recover the time-evolved form that we derived before. It’s also possible to derive a closed-form expression for the propagator of the simple harmonic oscillator; I won’t repeat the derivation here because it’s not very enlightening, but you can find it in Sakurai.
Propagators can be joined together (or split apart) in a simple way; if we insert a complete set of position states into the definition of a single propagator, we see that K(x',t; x, t_0) = \int d^3 x'' \bra{x'} e^{-i \hat{H} (t - t')/\hbar} \ket{x''} \bra{x''} e^{-i \hat{H} (t'-t_0)/\hbar} \ket{x} \\ = \int d^3 x'' [K(x',t; x'', t') \times K(x'', t'; x, t_0)].
If we switch for a moment to the Heisenberg picture, there’s another, possibly more intuitive way to represent exactly what the propagator is. Writing out the definition and doing some manipulations, we see that K(\vec{x}', t; \vec{x}, t_0) = \sum_a \left\langle \vec{x}' | a \right\rangle \left\langle a | \vec{x} \right\rangle \exp \left[ \frac{-i E_a (t-t_0)}{\hbar} \right] \\ = \sum_a \bra{\vec{x}'} \exp \left( -\frac{i\hat{H} t}{\hbar} \right) \ket{a} \bra{a} \exp \left( \frac{i \hat{H} t_0}{\hbar} \right) \ket{\vec{x}} \\ = \left\langle \vec{x}', t | \vec{x}, t_0 \right\rangle. (You can tell we’ve switched to the Heisenberg picture because we’re allowing the basis kets of \hat{x} to depend on time!) So the propagator is nothing more than the overlap of position ket \ket{\vec{x}} at time t_0 with a different position ket \ket{\vec{x}'} at later time t. This overlap is known as the transition amplitude between these two states; taking the squared absolute value gives us the probability that, given we have observed the particle at \vec{x} at time t_0, we will find has transitioned to \vec{x}' at time t.
Let’s stick with Heisenberg picture for now, since it makes writing the propagator easier, and it also treats time and space a little more equally in the notation. It also makes certain properties seem much more obvious, like the composition property which we derived above, which just amounts to inserting a complete set of states: \left\langle \vec{x}', t' | \vec{x}, t \right\rangle = \int d^3 x'' \left\langle \vec{x}', t' | \vec{x}'', t'' \right\rangle \left\langle \vec{x}'', t'' | \vec{x}, t \right\rangle.\ \ (t < t'' < t') Note that there’s no integral over time, just space; in the Heisenberg picture any operator commutes with itself at the same time, so we find the equal-time completeness relation \int d^3 x\ \ket{\vec{x}, t} \bra{\vec{x}, t} = 1.
Time evolution can be tricky to think about in quantum mechanics, and the propagator formalism makes certain questions much easier to answer.
25.2.1 Example: the Moshinsky quantum race
An interesting application of the free-particle propagator is to a very simple experiment which sheds some light on the time evolution of particles in a quantum system, known as the Moshinsky quantum race. The idea is simple: we produce an (approximately) monochromatic beam of non-interacting particles, with some mass m and energy E, which we can describe as a plane-wave state with wave number k = \sqrt{2mE}/\hbar. The beam is sent into a barrier with a movable shutter in the center:
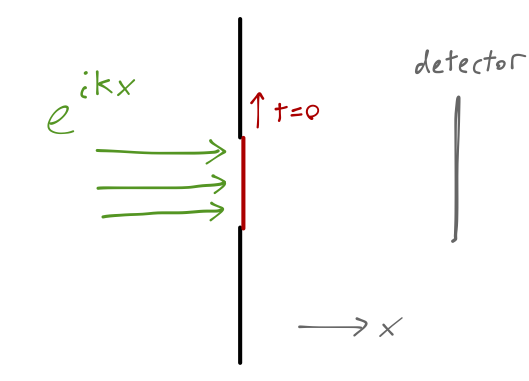
Until t=0, the shutter is closed and the wavefunction remains localized on the left side of the screen (x<0.) At t=0, we open the shutter; what does the profile of the traveling wave look like as time evolves? If we put a detection screen at some distance in front of the shutter, what will we observe?
The propagator makes these questions very straightforward to answer. The initial wavefunction is a plane wave trapped on the left side of the barrier, or \psi(x,0) = \Theta(-x) e^{ikx}. The wavefunction at time t is then just given by integrating this with the free propagator: \psi(x,t) = \int_{-\infty}^\infty dx' K_{\textrm{free}}(x,t; x',0) \psi(x',0) \\ = \sqrt{\frac{m}{2\pi i \hbar t}} \int_{-\infty}^0 dx' \exp \left[ \frac{i}{\hbar} \left( \frac{m (x-x')^2}{2t} + \hbar kx' \right) \right] Since we have an integral from -\infty to 0 and the function isn’t even in x', this is a bit more complicated than just a Gaussian integral, but it’s not too bad; Mathematica or some careful pen-and-paper work will give you the result \psi(x,t \geq 0) = \frac{1}{2} \exp \left( ikx - i k^2 \tau \right) {\rm erfc} \left( \frac{x-k\tau}{\sqrt{2i \tau}} \right) where \tau \equiv \hbar t/m. “Erfc” is the complementary error function, equal to 1 minus the integral of a Gaussian curve; it looks like a smoother version of the Heaviside step function, equal to 1 at large, negative arguments and 0 for large and positive arguments. (It tends to show up in cases like this where we integrate over Gaussian integrands but not over the full range of x.) The total solution is a convolution of this smoothed-out step shape with a plane wave, and looks something like this:
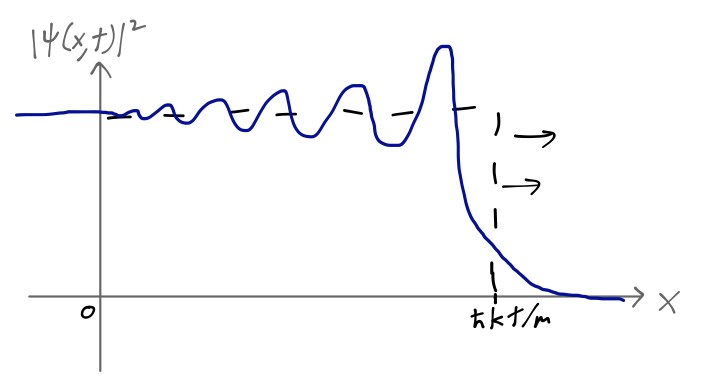
The wavefront here, defined as the point where the error function argument is zero, is at x = k \tau = \hbar k t / m = pt/m, exactly how a classical particle would move. In the classical limit \hbar \rightarrow 0, the error function becomes infinitely steep, and we find a perfectly localized “wavefront”, corresponding to the leading edge of the classical beam.
Quantum mechanically, this edge is smeared out; once we localized the wave at x=0, t=0, the evolution of different momentum components as a wave packet caused some spreading to occur. Still, if we performed the experiment of putting the screen in front of the shutter, we would find roughly zero probability of a particle hitting the screen for t < mx/\hbar k, and roughly unit probability for t > mx/\hbar k.
25.2.2 Example: the double-slit experiment
Another nice application of the free propagator is to one of the first experiments you probably encountered in discussing quantum mechanics, which is the double-slit experiment:
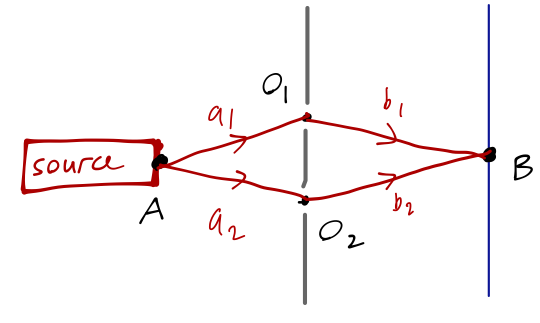
The wavefunction at point B on the screen at time t is given precisely by the propagator from the source at A, \left\langle B, t | A, 0 \right\rangle. We can decompose this propagator into the product of propagators from A to the barrier, and from the barrier to B. However, there are two possible paths now; the particle can either go through the upper opening O_1, or the lower opening O_2. From a probability point of view, these are completely independent events; the particle either goes through O_1 or O_2. Thus, the total probability amplitude can be written as a sum, \left\langle B,t | A,0 \right\rangle = \int_0^t dt_1 \left\langle B,t | O_1,t_1 \right\rangle \left\langle O_1,t_1 | A,0 \right\rangle + \int_0^t dt_2 \left\langle B,t | O_2,t_2 \right\rangle \left\langle O_2,t_2 | A,0 \right\rangle. This may look confusing at first; above, I said there is a spatial integration but no time integration when inserting a complete set of states. But now I’m writing just the opposite! What gives? Both are a result of the specific experimental setup here, in which we’re requiring our particle to propagate through the points O_1 or O_2. The positions of these openings collapse our integral over intermediate position to just the sum over O_1 and O_2 shown above. As for the time integration, that has been added to account for the fact that although our particles must pass through O_1 or O_2, the precise time at which they do so will vary depending on their speed. We could simplify by specifying a perfectly monochromatic source, i.e. fixed momentum, which would then fix t_1 and t_2 and remove the integrals.
Each of the four individual propagators is nothing more than the free-particle propagator, for example \left\langle O_1,t_1 | A,0 \right\rangle = \left( \frac{m}{2\pi i \hbar t_1} \right) \exp \left( \frac{im a_1^2}{2\hbar t_1} \right) where I’m writing the propagator now in two dimensions, and a_1 is the distance from A to O_1. Thus, the product under the first integral becomes \left\langle B,t | O_1,t_1 \right\rangle \left\langle O_1,t_1 | A,0 \right\rangle = \left( \frac{m^2}{4\pi^2 \hbar^2 t_1 (t-t_1)} \right) \exp \left[ \frac{im}{2\hbar} \left( \frac{a_1^2}{t_1} - \frac{b_1^2}{t-t_1} \right) \right] This is somewhat painful to integrate over, but if we plot the real part of the plane wave, we notice that as a function of the form e^{ix^2}, it looks something like this:
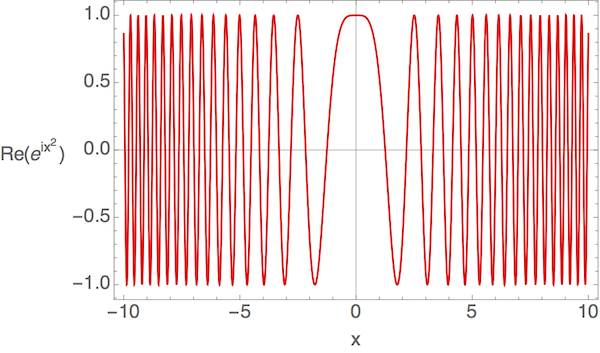
This function rapidly oscillates around zero if x is large, and so does the imaginary part. So we will find, on average, zero contribution to the integral from large values of x. The integral should thus be dominated by the points where the argument of the exponential is near zero. Here, if we take a_1 \approx b_1, these points will be where t_1 \approx t-t_1. In fact, if we make the assumption that t_1 \approx t/2, we can rewrite the expression in the form \int_0^t dt_1 \left\langle B,t | O_1,t_1 \right\rangle \left\langle O_1,t_1 | A,0 \right\rangle \approx \left( \frac{m^2}{\pi^2 \hbar^2 t^2} \right) \exp \left[ \frac{im}{\hbar t} (a_1 - b_1) (a_1 + b_1) \right]
I leave it as an exercise to show that by taking approximations like the above in the appropriate way, for all four lengths a_i and b_i approximately equal (but not exactly equal) we find that the squared propagator takes on the familiar form of an interference pattern, |\left\langle B,t | A,0 \right\rangle|^2 \propto 1 + \cos \left( \frac{m (\ell_1 - \ell_2) (\ell_1 + \ell_2)}{2\hbar t} \right) \sim \cos^2 \left( \frac{m (\ell_1 - \ell_2) (\ell_1 + \ell_2)}{4\hbar t} \right). where \ell_i = a_i + b_i is the total path length through each of the two slits.
Note: the 1/t may look funny, but remember that this is the propagator, which is only equal to the wavefunction if our initial state is really \ket{A,0}, i.e. a sharp delta function localized at the source at time t=0. In this case, we expect non-trivial time dependence. If we have a steady-state source, we would remove t by identifying it as the time of flight from the source, t = \frac{\ell}{v} = \frac{m\ell}{p} = \frac{m\ell}{\hbar k} where \ell = (\ell_1 + \ell_2) / 2, so |\left\langle B,t | A,0 \right\rangle|^2 \sim \cos^2 \left( \frac{k}{2} (\ell_1 - \ell_2) \right) = \cos^2 \left( \frac{\pi (\ell_1 - \ell_2)}{\lambda} \right), matching the textbook result based on wave interference.
25.3 Path integration
We could at this point imagine generalizing this approach to deal with more complicated variants of the same problem. For example, if we had a barrier with three holes, or four, or N we could still find the final interference pattern just by summing over the possible propagator combinations: \left\langle B,t | A_0 \right\rangle = \sum_{i=1}^N \int_0^t dt_i \left\langle B,t | O_i,t_i \right\rangle\left\langle O_i,t_i | A,0 \right\rangle.
25.3.1 A thought experiment: removing the screen
As this thought experiment becomes more complicated, it starts to lead us in an interesting direction. What if we added a second barrier in between the first and the detector?
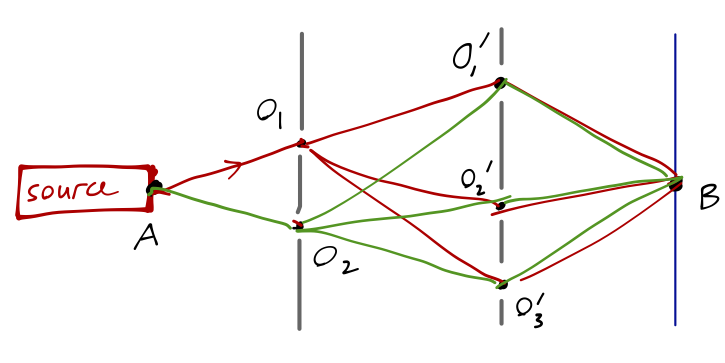
The events of the particle passing through any hole in any barrier are still all independent, so we can write the overall amplitude as a more complicated sum, decomposing into propagators from A to O_i to O'_j to B. While the sum has more terms, the basic idea is the same: the amplitude to travel any one path is just the product of the propagators along each piece of the path. At this point, it’s easy to imagine adding more barriers and more holes; the sum gets more complicated, but the basic principle remains the same - just sum over the propagator products for all possible paths from A to B.
Now here is the important realization: if we take the limit where the number of holes in the barrier goes to infinity, so that there really isn’t any barrier at all, then we’re left with nothing but a particle propagating through empty space! But as we take the limit, we’re still carefully summing over all of the number of possible paths, now approaching infinity. So screens or not, the probability amplitude for a particle to propagate from x to y in time T is equal to the sum over all possible paths from x to y. This was Richard Feynman’s key insight into a new way of formulating quantum mechanics.
Let’s go back to our rigorous definitions now. How do we formally describe such a “sum over paths”? Let’s start by considering the interval from some initial time t_1 to final time t_N, which we’ll subdivide into N-1 equal steps in between: t_j - t_{j-1} = \frac{t_N - t_1}{N-1}. We’ll also call the initial position x_1 and the final position x_N. With no screens in the middle, we want to continuously average over the paths, so the sums become integrals: \left\langle x_N, t_N | x_1, t_1 \right\rangle = \int dx_{N-1} \int dx_{N-2} ... \int dx_2 \\ \hspace{40mm} \left\langle x_N, t_N | x_{N-1}, t_{N-1} \right\rangle \left\langle x_{N-1}, t_{N-1} | . \right\rangle.. \left\langle x_2, t_2 | x_1, t_1 \right\rangle. (If you like, this is sort of equivalent to the limit where we still have N screens, but each screen has an infinite number of holes so there is no screen left.) You’ll immediately recognize this as just the application of the composition of propagators, as we defined above. In fact, we could have skipped the digression and just gone right to this equation, as Sakurai does. But I wanted to make the “sum over paths” idea a bit more clear. You should also suspect that this will be a particularly useful way to think about the case where \hat{H} depends explicitly on time (imagine a different \hat{H} appearing in each of the infinitesmal propagators.)
25.3.2 The path integral
Now we’re ready to return to the quantum expression for the propagator. Notice that we can rewrite each of the intermediate propagators by pulling out the time evolution to find \left\langle x_j, t_j | x_{j-1}, t_{j-1} \right\rangle = \bra{x_j} \exp \left( - \frac{i\hat{H} \Delta t}{\hbar} \right) \ket{x_{j-1}}. Since we’re studying the evolution of a single particle, let’s split the Hamiltonian up into the kinetic and potential energy terms, \hat{H} = \frac{\hat{p}^2}{2m} + V(\hat{x}). Since \hat{x} and \hat{p} don’t commute, normally we wouldn’t be able to split up the exponential. But since we’re dealing with the infinitesmal time-step \Delta t, we can rewrite \exp \left( -\frac{i\hat{H} \Delta t}{\hbar} \right) = \exp \left( -\frac{i \hat{p}^2 \Delta t}{2m \hbar} \right) \exp \left( -\frac{i V(\hat{x}) \Delta t}{\hbar} \right) + \mathcal{O}(\Delta t^2). Inserting a complete set of states then gives \left\langle x_j, t_j | x_{j-1}, t_{j-1} \right\rangle = \int dx' \bra{x_j} \exp \left( -\frac{i \hat{p}^2 \Delta t}{2m\hbar} \right) \ket{x'} \bra{x'} \exp \left( -\frac{i V(\hat{x}) \Delta t}{\hbar} \right) \ket{x_{j-1}} \\ = \int dx' \bra{x_j} \exp \left( -\frac{i \hat{p}^2 \Delta t}{2m\hbar} \right) \ket{x'} \exp \left( -\frac{i V(x_{j-1}) \Delta t}{\hbar} \right) \delta(x' - x_{j-1}). The first expression is just the free-particle propagator which we’re now familiar with, and the delta function from the second term collapses the integral, so we have \left\langle x_j, t_j | x_{j-1}, t_{j-1} \right\rangle = \sqrt{\frac{m}{2\pi i \hbar \Delta t}} \exp \left[ \left( \frac{m(x_j - x_{j-1})^2}{2 (\Delta t)^2} - V(x_{j-1}) \right) \frac{i \Delta t}{\hbar} \right].
(As a very brief aside, this equation has exactly the sort of form that would be useful for setting up numerical solutions of quantum time evolution in the usual way, by evaluating finite differences repeatedly.) Plugging back in to the full propagator above, we thus find \left\langle x_N, t_N | x_1, t_1 \right\rangle = \left( \frac{m}{2\pi i \hbar \Delta t}\right)^{(N-1)/2} \int dx_{N-1} dx_{N-2} ... dx_2 \\ \exp \left[ \frac{i \Delta t}{\hbar} \sum_{j=2}^{N-2} \left(\frac{1}{2} m \left( \frac{x_{j+1} - x_j}{\Delta t}\right)^2 - V(x_j) \right) \right] Finally taking the limit \Delta t \rightarrow 0, the difference becomes a derivative and the sum an integral:
The formal solution to the propagator for a general quantum system can be written in terms of the Feynman path integral,
\lim_{\Delta t \rightarrow 0} \left\langle x_N, t_N | x_1, t_1 \right\rangle = \int \mathcal{D}[x(t)] \exp \left[ \frac{i}{\hbar} \int_{t_1}^{t_N} dt \left( \frac{1}{2} m \dot{x}(t)^2 - V(x(t)) \right) \right]. \\ = \int_{x_1}^{x_N} \mathcal{D}[x(t)] \exp \left[ \frac{i}{\hbar} \int_{t_1}^{t_N} dt\ \mathcal{L}(x, \dot{x}) \right] \\ = \int_{x_1}^{x_N} \mathcal{D}[x(t)] \exp \left[ \frac{iS(x,\dot{x})}{\hbar} \right]. The script D denotes the “path integration” itself, which is the properly-normalized infinite-dimensional limit of our interval subdivision, \int_{x_1}^{x_N} \mathcal{D}[x(t)] \equiv \lim_{N \rightarrow \infty} \left( \frac{m}{2\pi i \hbar \Delta t} \right)^{(N-1)/2} \int dx_{N-1} \int dx_{N-2} ... \int dx_2. The quantity S = \int dt\ \mathcal{L} is the action, the same function which appears mysteriously in the derivation of the Lagrangian framework in classical mechanics.
The path integral provides us with a very intuitive way of seeing how classical mechanics arises from quantum mechanics, and in particular why a classical system should satisfy the principle of least action. Suppose we want to compare the contribution of two paths to the overall propagator, one with action S_0, and another with action S_0 + \delta S. As we’ve seen, the total contribution is the sum over the paths of e^{iS/\hbar}, i.e. \exp \frac{i S_0}{\hbar} + \exp \left(\frac{i (S_0 + \delta S)}{\hbar} \right) = e^{iS_0 / \hbar} \left(1 + e^{i \delta S / \hbar} \right). If we average over many paths, “integrating” over \delta S in the formal sense, we see that if the changes in action are large compared to \hbar, then the phase will oscillate wildly; as the phase varies, it will go from 1 to -1 and anywhere in between in the complex plane, and we can find large cancellations. The only sets of paths which will contribute significantly, similar to what we saw in the two-slit example above, are those which add coherently, i.e. for which \delta S \approx 0. Turning points of the action, where \delta S changes slowly as the path is deformed, are exactly those paths given by the Euler-Lagrange equations; they are the classical paths.
Path integrals are a radically different-looking way to formulate quantum mechanics, but one which is equivalent to the Schrödinger approach we’ve been working in. In fact, it’s straightforward to go in the opposite direction: start with the path integral and derive the time-dependent Schrödinger equation.
We can even solve for the dynamics of quantum systems using the path integral, at least in principle. As Sakurai points out, the path integral can be exactly evaluated for the simple harmonic oscillator, giving the propagator (and with a little more work, the energy eigenfunctions and corresponding energy levels.) Unfortunately, the path integral is intractable for all but the simplest non-relativistic quantum systems. Our goal will mostly be to use it as a formal construct, to give us useful insights into gauge symmetry that are much more obscure without the path integral.
In quantum field theory and statistical mechanics, the path integral sees much more practical use. In fact, there is a subfield known as lattice field theory which turns the infinite-dimensional path integral into a finite-dimensional object by discretizing space and time into a finite lattice, and then uses Monte Carlo methods to evaluate the path integral numerically. But that’s a story for another class!
25.3.3 WKB and path integration
Since we’ve seen both now, it’s interesting to make a quick connection between WKB approximation and the path integral formulation of quantum mechanics. The path integral gave us an expression for the propagator, K(x',t';x, t) = \int_{x}^{x'} \mathcal{D}[x(t)] \exp \left[ \frac{i}{\hbar} \int_{t}^{t'} dt\ \mathcal{L}(x,\dot{x}) \right]. As we know, the classical solution for the motion in a given system corresponds to a turning point of the action S = \int dt\ \mathcal{L}; the contributions of paths near the classical path constructively interfere.
This means that the path integral will be dominated by paths close to the classical solution x_{\rm cl}. We can expand x = x_{\rm cl} + y, and then rewrite as an integration over the small differences y = x - x_{\rm cl} to the classical trajectory, K = \int \mathcal{D}[y] \exp \left[ \frac{i}{\hbar} \int_{t}^{t'} dt\ \mathcal{L}(x_{\rm cl} + y, \dot{x}_{\rm cl} + \dot{y}) \right] This can be expanded out in terms of variations of the action \delta S, but rather than getting too far into the details, we’ll just work with the leading-order approximation, which is that the result of the integration is just result of the classical path: K(x',t'; x, t) \approx C \exp \left[ \frac{i}{\hbar} \int_t^{t'} dt\ \mathcal{L}(x_{\rm cl}, \dot{x}_{\rm cl}) \right]. We’re working with Schrödinger’s equation in an arbitrary potential, which means we’ve explicitly assumed the form of the Lagrangian is \mathcal{L}(x, \dot{x}) = \frac{1}{2} m \dot{x}^2 - V(x). Now, for the WKB approximation we are working with energy eigenstate solutions \psi_E(x), which means we’ve separated out the time dependence from the spatial dependence in the wavefunction. To make this more explicit in the current approach, we assume our classical solution corresponds to total energy E. We know the relationship between the classical solution and the energy: E = \frac{1}{2}m \dot{x}_{\rm cl}^2 + V(x_{\rm cl}), which lets us eliminate the potential in favor of the energy: K(x',t'; x,t) \approx C \exp \left[ \frac{i}{\hbar} \int_{t}^{t'} dt\ \left( m \dot{x}_{\rm cl}^2 - E \right) \right] \\ = C \exp \left[ \frac{im}{\hbar} \int_{t}^{t'} dt\ \dot{x}_{\rm cl}^2 \right] \exp \left[ \frac{iE (t'-t)}{\hbar} \right], splitting the time-dependence out in the expected form. Focusing on the remaining part, since we know what we’re working towards, let’s rewrite one of the two velocity terms using p \equiv m \dot{x}_{\rm cl}. Using the other to swap limits of integration, K(x',t'; x,t) \approx C \exp \left[ \frac{i}{\hbar} \int_x^{x'} dx\ p(x) \right] \exp \left[ \frac{iE (t'-t)}{\hbar} \right]. Since the temporal and spatial parts are fully separated, we can read off the evolution for the spatial wavefunction from the first part: recalling that \psi(x',t') = \int dx'' K(x', t'; x'',t) \psi(x'',t) we can just insert a delta function for the initial spatial wavefunction to obtain \psi(x',t') \sim C \exp \left[ \frac{iEt'}{\hbar} \right] \exp \left[ \frac{i}{\hbar} \int_x^{x'} dx\ p(x) \right].
This more or less recovers our WKB wavefunction above, except that we’re missing the 1/\sqrt{k(x)} that came from the next-to-leading order term in the \hbar expansion. This is exactly what we’ve discarded by just keeping the classical action; if we go back and carefully do the path integral over the path variations y(t), we will find a Gaussian integral that we can evaluate to get the 1/\sqrt{k} and recover the WKB approximation in full.