32 Electromagnetic transitions in atoms and molecules
Now that we’ve gone through the effort of setting up the machinery, we’re prepared to go through a number of examples that show how time-dependent perturbation theory and semiclassical electromagnetism can be used to describe realistic transitions in atoms and molecules. This finally opens up to us a complete description of what experimental measurements observe in terms of spectral lines, which correspond to light emitted in specific transitions between energy levels. The wavelength of a given spectral line tells us the energy splitting between the two levels involved in the transition, but now we can finally add a prediction for the intensity of spectral lines, which is related to the rate at which the transition happens. Specifying the mechanism of the transition also lets us apply selection rules to explain why some energy-level differences will not appear in the emission spectrum.
32.1 Example: vibrational modes of diatomic molecules
Let’s start with a molecular example. The vibrational modes of a diatomic molecule such as OH can be reasonably described by a one-dimensional simple harmonic oscillator potential, \hat{H}_0 = \frac{\hat{p}^2}{2m} + \frac{1}{2} m \omega_0^2 \hat{x}^2.
We already looked briefly at this for a generic harmonic perturbation, but now let’s consider specifically spontaneous emission. Adopting the result we already had for the differential rate, we have in dipole approximation \frac{dW_{\gamma,fi}}{d\Omega_k} = \frac{\hbar e^2}{2\pi c^3 m^2 \omega} \int dE_f \rho_f(E_f) \sum_{\epsilon} \left| \frac{m \omega_{if}}{\hbar} \bra{f} \vec{\epsilon} \cdot \hat{\vec{r}} \ket{i} \right|^2 \omega_{if}^2. We haven’t picked any coordinates yet, so without loss of generality we just take the \hat{\vec{r}} vector to point in the \hat{x} direction, along the axis of the molecule. (If we have a gas of molecules with random orientations, we should integrate over this direction, but we will integrate over the emitted photon angle anyway so any difference will be washed out.) Doing the polarization sum gives (1 - \cos^2 \theta_k) as before, so that we can integrate over the photon angle to find W_{\gamma,fi} = \frac{4 e^2}{3c^3 \hbar \omega} \int dE_f\ \rho_f(E_f) \omega_{if}^4 |\bra{f} \hat{x} \ket{i}|^2. The transition matrix element connects state \ket{n} with states \ket{n \pm 1}, as we found before: |\bra{f} \hat{x} \ket{i}|^2 = \frac{\hbar}{2m\omega_0} ( (n+1) \delta_{n,n+1} + n \delta_{n,n-1}) Since we’re looking specifically at spontaneous emission, the energy of the final state has to be lower, so we must have \ket{f} = \ket{n-1}, the second term above. The density of states is also fully discrete, \rho_f(E_f) = \sum_n \delta(E_f - \hbar \omega (n + \tfrac{1}{2})). Finally, since we can only jump by one energy level, the energy splitting is fixed and independent of n: \omega_{if} = \omega_{n,n-1} = \omega_0. Putting everything together, then, the result for the rate is \Gamma_n = \frac{4e^2}{3c^3 \hbar \omega_0} \frac{\hbar}{2m\omega_0} n \omega_0^4 = \frac{4\hbar \alpha \omega_0^2}{3mc^2}n. We see that while the emitted energy of the photon is the same for all energy levels due to the equal spacing in the harmonic oscillator, \hbar \omega = \hbar \omega_0, the rate grows linearly with the state number n; the transition 2 \rightarrow 1 is twice as fast as the transition 1 \rightarrow 0.
Here I would try to make a comparison to experiment, but data on purely vibrational transitions in diatomic molecules is hard to come by; in practice, a realistic description requires a simultaneous study of rotation along with vibration (producting the “ro-vibrational spectrum”), and selection rules typically require angular momentum to change along with vibrational mode. The prediction we’ve written down here would, in principle, apply to what are known as “Q branch” transitions where angular momentum remains fixed. For now, we’ll treat this as a warm-up and stop here with this calculation.
32.2 Spontaneous emission in hydrogen-like atoms
Next, let’s consider spontaneous emission from hydrogen and hydrogen-like atoms. We’ll continue to work in dipole approximation. We know that the initial-state and final-state wavefunctions can be broken apart according to their quantum numbers as \psi_{nlm}(\vec{r}) = R_{nl}(r) Y_l^m(\theta, \phi). The matrix element needed for a dipole transition from \ket{i} = \ket{n_i l_i m_i} to \ket{f} = \ket{n_f l_f m_f}, then, is \bra{f} \hat{\vec{r}} \ket{i} = \bra{n_f l_f m_f} \hat{\vec{r}} \ket{n_i l_i m_i}. Here we’ll work in a spherical basis, writing \vec{r} = \sum_q \hat{e}_q^\star r_q^{(1)} where the spherical components of the position vector are, as a reminder, r_q^{(1)} = \sqrt{\frac{4\pi}{3}} r Y_1^q(\theta, \phi). Then we have for the component matrix elements \bra{n_f l_f m_f} \hat{r}_q^{(1)} \ket{n_i l_i m_i } = \int dr\ R_{n_f l_f}^\star(r) R_{n_i l_i}(r) r^3 \int d\Omega Y_{l_f}^{m_f}{}^\star(\theta, \phi) \sqrt{\frac{4\pi}{3}} Y_1^q(\theta, \phi) Y_{l_i}^{m_i}(\theta \phi) \\ = I_R \sqrt{\frac{(2l_i+1)}{(2l_f+1)}} \left\langle l_i 1;00 | l_i 1;l_f 0 \right\rangle \left\langle l_i 1;m_i q | l_i 1;l_f m_f \right\rangle, writing I_R for the result of the radial integral, and using the identity we derived for triple spherical-harmonic integrals back in Section 27.3.1. But from the second Clebsch-Gordan coefficient, as discussed in the previous section, we can read off two selection rules: |l_i-1| \leq l_f \leq l_i \pm 1; \\ m_f = m_i + q. In fact, in dipole approximation l_f = l_i is also forbidden, due to parity; \vec{r} itself is odd under parity, so for the whole matrix element to be parity-even, l_f = l_i \pm 1. The other quantum number q can only vary between -1 and +1, so we also see that m_f = m_i \pm 1 or m_f = m_i.
All of this was completely ignoring the electron spin; we know that in our initial Hamiltonian, the wavefunctions should really be written as \ket{nlmm_s}. Since the perturbation doesn’t couple to spin at all, we have the further selection rule \Delta m_s = 0. But this is a choice we’ve made for what the unperturbed Hamiltonian \hat{H}_0 is! If we want to study the hydrogen atom including fine-structure effects, or hydrogen in a strong magnetic field, we know a better choice of basis is total angular momentum \vec{J} = \vec{L} + \vec{S}, in which case the basis states are \ket{nljm}.
Putting these statements together, even before we compute anything quantitative, we have an important result:
Working in the dipole approximation, spontaneous emission transitions in hydrogen are only allowed between states for which \Delta l = \pm 1 (in the \ket{nlmm_s} basis), or \Delta j = \pm 1 (in the \ket{nljm} basis.) In either case, we must also have |\Delta m| \leq 1.
With this result for the matrix element, we can plug in to the results we found before to write a formula for the differential rate: \frac{dW_{i \rightarrow f}}{d\Omega_k} = \frac{\omega^3 e^2}{2\pi \hbar c^3} \sum_{\epsilon} |\bra{f} \vec{\epsilon} \cdot \hat{\vec{r}} \ket{i}|^2 or doing the full angular integration with the polarization sum, W_{i \rightarrow f} = \frac{4\alpha \omega^3}{3c^2} |\bra{f} \hat{\vec{r}} \ket{i}|^2. We’ll focus here mainly on the total rate (final formula), but I showed both formulas since there is additional information that can be useful in the differential rate dW/d\Omega_k that can tell us more about the quantum numbers of the states involved in the transition if we measure it.
So far, this is also written for a single transition between two energy eigenstates, but often we want to sum over several degenerate states, for example to compute an overall 2p \rightarrow 1s transition rate by summing over the m_i and m_f. In all such cases, we know the rule: we average over all initial states and sum over all final states. So for example, W_{n_i l_i \rightarrow n_f l_f} = \frac{4\alpha \omega^3}{3c^2} \frac{1}{2l_i + 1} \sum_{m_i} \sum_{m_f} |\bra{n_f l_f m_f} \hat{\vec{r}} \ket{n_i l_i m_i}|^2 \\ = \frac{4\alpha \omega^3}{3c^2} \frac{1}{2l_i + 1} \sum_{m_i} \sum_{m_f} \sum_{q=-1}^{1} |\bra{n_f l_f m_f} \hat{r}_q^{(1)} \ket{n_i l_i m_i}|^2 passing to spherical tensor notation on the last step. Although there is a formal sum over the index q present, in practice rotational symmetry requires m_f = m_i + q, which means that only one term will survive for a given pair \{m_i, m_f\}.
This is an obvious place where we can use the Wigner-Eckart theorem, to write this instead in terms of a single reduced matrix element \bra{n_f l_f} |\hat{\vec{r}}^{(1)}| \ket{n_i l_i} instead of calculating all of the terms separately.
32.3 Example: S \rightarrow P transitions in a strong magnetic field
Let’s have a closer look at the case of a transition in hydrogen with a magnetic field applied to split the states apart. In this case (known as Zeeman splitting, see Section 28.4), the appropriate quantum numbers are \ket{nljm}, and the energy levels are E_{njm} = E_n^{(0)} + \Delta_{jm}^{(1)} = -\frac{1}{n^2} {\rm Ry} + \frac{eB}{2m_e c} g_j \hbar m \equiv -\frac{1}{n^2} {\rm Ry} + E_B g_j m, defining E_B as the energy associated with the magnetic field and with g_j the Landé g-factor, g_j = \begin{cases} 1 + \frac{1}{2l+1}, & j = l + 1/2; \\ 1 - \frac{1}{2l+1}, & j = l - 1/2. \end{cases}
Before we think about transitions, let’s remind ourselves of what the spectrum looks like. For concreteness let’s say that we’re looking at the 3s \rightarrow 2p transition, although everything we’re about to do generalizes easily to other values of n. In modified spectroscopic notation (dropping the spin label which is always 2), the available energy levels are 3s_{1/2} (two states), 2p_{1/2} (two states), and 2p_{3/2} (four states). Each state is split completely, with g-factors of 2, 2/3, and 4/3 respectively. There is also a large splitting between the n=3 energy level and the n=2 levels. Here is a sketch of the energy levels available:
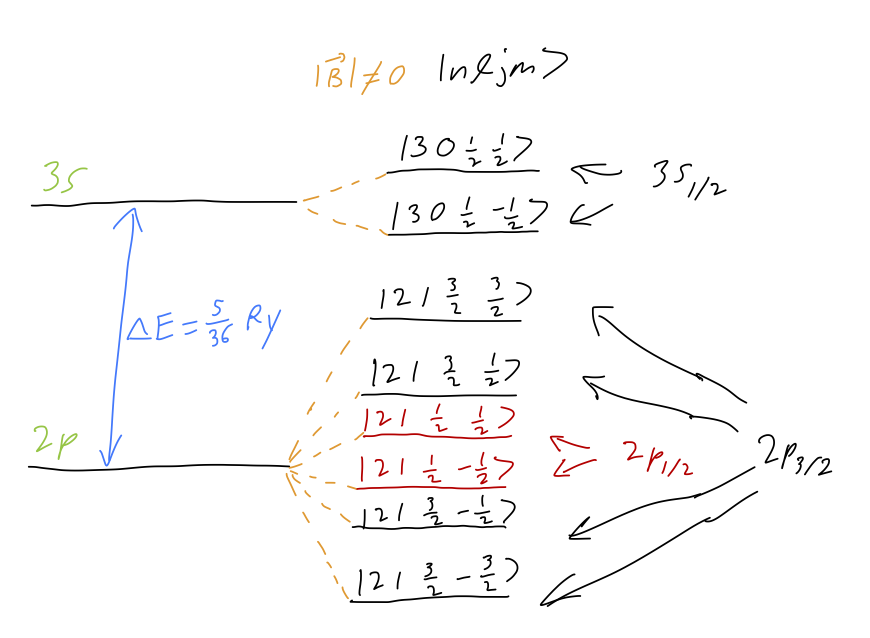
The dominant energy splitting is due to the difference in principal energy levels, \Delta E_0 = (\frac{1}{3^2} - \frac{1}{2^2}) Ry = 5/36 Ry. There are 12 total transitions, but some of them are forbidden: in particular, the two \ket{j=3/2, m = \pm 3/2} levels can’t be reached from \ket{j=1/2, m=\mp 1/2} due to the \Delta m selection rule. Thus, we expect 10 emission lines in total. (We are ignoring transitions between the two 2p levels; they are certainly possible due to the Zeeman splitting, but they will be in a completely different frequency range from the 3 \rightarrow 2 transitions.)
To compute the rates for the transitions, we need the relevant matrix elements. Invoking the Wigner-Eckart lets us write them all in terms of two reduced matrix elements: we have \bra{21\tfrac{1}{2} m_f} \vec{r}_q^{(1)} \ket{30\tfrac{1}{2} m_i} = \left\langle \tfrac{1}{2} 1; m_i q | \tfrac{1}{2} 1;\tfrac{1}{2} m_f \right\rangle \frac{\bra{n=2,j=\tfrac{1}{2}} |\vec{r}| \ket{n=3,j=\tfrac{1}{2}}}{\sqrt{2}}, \\ \bra{21\tfrac{3}{2} m_f} \vec{r}_q^{(1)} \ket{30\tfrac{1}{2} m_i} = \left\langle \tfrac{1}{2} 1;m_i q | \tfrac{1}{2} 1;\tfrac{3}{2} m_f \right\rangle \frac{\bra{n=2,j=\tfrac{3}{2}} |\vec{r}| \ket{n=3,j=\tfrac{1}{2}}}{2}.
Let’s denote the two reduced matrix elements as R_{1/2} \equiv \bra{n=2,j=\tfrac{1}{2}} |\vec{r}| \ket{n=3,j=\tfrac{1}{2}}, \\ R_{3/2} \equiv \bra{n=2,j=\tfrac{3}{2}} |\vec{r}| \ket{n=3,j=\tfrac{1}{2}}. To actually compute these reduced matrix elements, we need to compute one of the matrix elements in full, which means doing radial integrals. Here, we’ll stick to working out the relative intensity of the spectrum, which just depends on the Clebsch-Gordan coefficients.
Let’s begin with the 3s_{1/2} \rightarrow 2p_{1/2} transitions. We have four possible transition lines that we’ll denote a,b,c,d:
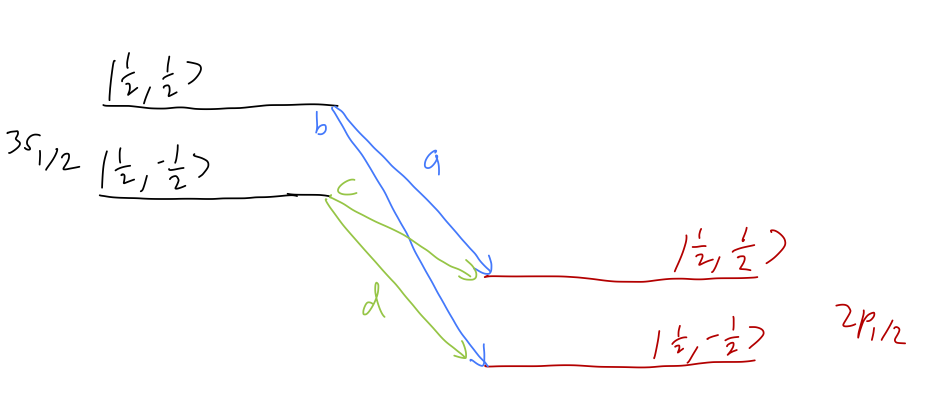
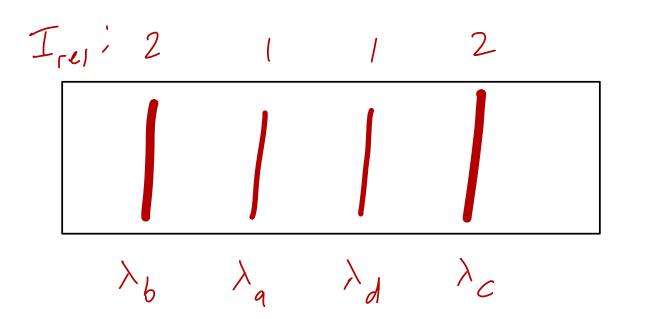
The corresponding matrix elements are, plugging in Clebsch-Gordans from a table, M_a = \frac{\left\langle \tfrac{1}{2} 1; \tfrac{1}{2}0 | \tfrac{1}{2} 1; \tfrac{1}{2} \tfrac{1}{2} \right\rangle}{\sqrt{2}} R_{1/2} = -\frac{1}{\sqrt{6}} R_{1/2}, \\ M_b = -\frac{1}{\sqrt{3}} R_{1/2}, \\ M_c = \frac{1}{\sqrt{3}} R_{1/2}, \\ M_d = \frac{1}{\sqrt{6}} R_{1/2}. To get the decay rates \Gamma, which are proportional to the intensities, we square these and add some other factors, for example \Gamma_a = \frac{4\alpha \omega_a^3}{3c^2} |M_a|^2 and so on. But if we want the relative intensity of the lines, everything cancels - including the reduced matrix element R_{1/2}. Only the ratios of Clebsch-Gordans squared matter. We can read off the result: I_a : I_b : I_c : I_d = 1 : 2 : 2 : 1. In other words, the two middle transition lines will be twice as bright as the other two. (Actually, this isn’t exactly right; the intensities also go as \omega^3, and the transition energies are slightly different. But they are all dominated by the energy-level change \Delta E_0, so the differences in frequency will be relatively small.)
If we were to look at the emission through a diffraction grating, we’ll be directly sensitive to the wavelength \lambda of each transition. What are the wavelengths corresponding to the transitions? Plugging in, \lambda_a = \frac{2\pi \hbar c}{\Delta E_a} = \frac{2\pi \hbar c}{\Delta E_0 + E_B/3} \\ \lambda_b = \frac{2\pi \hbar c}{\Delta E_0 + 5E_B/3} \\ \lambda_c = \frac{2\pi \hbar c}{\Delta E_0 - 5E_B/3} \\ \lambda_d = \frac{2\pi \hbar c}{\Delta E_0 - E_B/3}. So the wavelengths are ordered \lambda_b < \lambda_a < \lambda_d < \lambda_c. Assuming that the magnetic field contribution E_B is small, the approximate wavelength of all of them is \bar{\lambda} = \frac{2\pi \hbar c}{\Delta E_0} = \frac{2\pi (6.58 \times 10^{-16}\ {\rm eV} \cdot {\rm s}) (3 \times 10^8\ {\rm m/s})}{1.89\ {\rm eV}} \approx 660\ {\rm nm} which is red visible light. (Since we’ll use it in a moment, the corresponding angular frequency is \bar{\omega} = 2\pi c/\bar{\lambda} = 2.86 \times 10^{15}\ {\rm Hz}.) That means if we look through a diffraction grating, we’ll see a pattern like this:
Now suppose that we turn off our magnetic field and we’re just interested in the total rate \Gamma for the 3s \rightarrow 2p transition. This means that we have to sum and average over all of the possible initial and final states, as above: \Gamma_{3s \rightarrow 2p_{1/2}} = \frac{1}{2} \sum_{m_i} \sum_{m_f} \Gamma_{m_i \rightarrow m_f} \\ = \frac{2\alpha}{3c^2} (|M_a|^2 \omega_a^3 + |M_b|^2 \omega_b^3 + |M_c|^2 \omega_c^3 + |M_d|^2 \omega_d^3) \\ \approx \frac{2\alpha \bar{\omega}^3}{3c^2} |R_{1/2}|^2 \left( \frac{1}{6} + \frac{1}{3} + \frac{1}{3} + \frac{1}{6} \right) \\ = \frac{2\alpha \bar{\omega}^3}{3c^2} |R_{1/2}|^2.
Let’s evaluate the reduced matrix element to finish the calculation and get an actual number out. To find it, we invert the Wigner-Eckart theorem to write R_{1/2} = \frac{\sqrt{2}}{\left\langle \tfrac{1}{2} 1; m_i q | \tfrac{1}{2} 1; \tfrac{1}{2} m_f \right\rangle} \bra{2 1 \tfrac{1}{2} m_f} \hat{r}_q^{(1)} \ket{3 0 \tfrac{1}{2} m_i}. Now we’re free to pick any m_i, m_f, q that we want, as long as they satisfy the selection rule (if they don’t, we’ll know because the Clebsch-Gordan coefficient won’t exist.) Let’s take m_i = m_f = \tfrac{1}{2}, which then requires q=0: plugging in, R_{1/2} = -\sqrt{6} \bra{2 1 \tfrac{1}{2} \tfrac{1}{2}} \hat{r}_0^{(1)} \ket{3 0 \tfrac{1}{2} \tfrac{1}{2}}. The one remaining obstacle here is that this matrix element is written in the \ket{nljm} basis, but we only really know how to evaluate matrix elements as integrals in the \ket{nlm_lm_s} basis. (For fine structure we used various algebraic tricks to get around this.) Fortunately, we know how to change bases easily: \ket{3 0 \tfrac{1}{2} \tfrac{1}{2}} = \ket{300} \ket{\uparrow}, \\ \ket{2 1 \tfrac{1}{2} \tfrac{1}{2}} = \sqrt{\frac{2}{3}} \ket{211} \ket{\downarrow} - \sqrt{\frac{1}{3}} \ket{210} \ket{\uparrow} using the same C-G table again and splitting out the spin in the \ket{nlm_l m_s} states on the right to make them more easily distinguishable. Since the operator \hat{r} doesn’t talk to spin at all, the spin can’t change from initial to final state, and we have R_{1/2} = \sqrt{2} \bra{210} \hat{r}_0^{(1)} \ket{300} \\ = \sqrt{2} \int dr R_{21}^\star(r) R_{30}(r) r^3 \sqrt{\frac{1}{3}} \left\langle 01;00 | 01;10 \right\rangle \left\langle 01;00 | 01;10 \right\rangle using the identity we wrote out above to simplify the triple-Y integral. We need one more C-G coefficient, but this one is for addition of j=0, which means that the coefficent (which appears twice) is just 1, so at last, we have R_{1/2} = \sqrt{\frac{2}{3}} \int dr R_{21}(r) R_{30}(r) r^3. Going to Mathematica to evaluate this final integral, we have the result R_{1/2} \approx 0.766 a_0.
Finally, putting everything together and plugging in a_0 = 5.29 \times 10^{-11} m, \Gamma_{3s \rightarrow 2p_{1/2}} \approx \frac{2\alpha \bar{\omega}^3}{3c^2} |R_{1/2}|^2 \approx 2.1 \times 10^{6}\ {\rm Hz} or about 2.1 MHz. If we look this up in the NIST atomic spectra database, we find a transition frequency of 2.10 \times 10^6/s, so we’ve got it exactly right!
32.4 Line widths
There is one more important idea that we should discuss in the current context, which has to do with the lifetime of a state \ket{i}. If there are spontaneous transitions available for this state to some set of final states \{\ket{f}\}, then over time it will decay away. So far we know how to compute transition rates between states, but a more careful study of remaining in the same state requires us to revisit our Fermi’s golden rule calculation in a more careful way. As discussed previously, in quantum mechanics the initial state won’t obviously just irreversibly decay from \ket{i} \rightarrow \ket{f}: the reverse process \ket{f} \rightarrow \ket{i} is also allowed, so we can jump from \ket{i} \rightarrow \ket{f} \rightarrow \ket{i} and still remain in the initial state. The latter process is second-order in our perturbation (since it requires two transitions.)
Previously, I noted that constant perturbations in time-dependent perturbation theory can’t be thought of as truly constant; we should think of them being adiabatically switched on and off. To accomplish that more rigorously, let’s study a constant perturbation again but with an adiabatic damping factor applied: \hat{V}(t) = \hat{V} e^{\eta t}, with \eta a very small auxiliary variable that we will take to zero (carefully) to recover a constant perturbation. By construction this regulates things as t \rightarrow -\infty, which we’ll take to be our initial state; it blows up at t \rightarrow \infty, but we’ll just evolve to a finite time t and make sure we deal with the order of limits properly to get there.
32.4.1 Rederiving Fermi’s golden rule
Let’s start back at first-order again for a transition between states. For convenience, we’ll partly move to the interaction picture: we’ll compute the interaction transition amplitude U_{fi}^{(I)}(t), which absorbs the two phases that aren’t being integrated over: U_{fi}^{(I)}(t) = \delta_{fi} - \frac{i}{\hbar} \int_{t_i}^t dt' e^{i\omega_{fi} t'} e^{\eta t'} \bra{f} \hat{V} \ket{i} \\ = \delta_{fi} - \frac{i V_{fi}}{\hbar} \frac{1}{i\omega_{fi} + \eta} e^{(i\omega_{fi} + \eta)t}. Let’s assume that f \neq i to begin with, and square this to get the transition probability, p_{fi}(t) = |U_{fi}^{(I)}(t)|^2 = \frac{|V_{fi}|^2}{\hbar^2 (\omega_{fi}^2 + \eta^2)} e^{2\eta t}, and then the rate is W_{fi} = \lim_{t\rightarrow \infty} p_{fi}(t) / t. (Notice that the use of the interaction-picture amplitude is now equivalent to the regular amplitude, since the difference is just two phases that square away in the probability.) But now we have to be careful with the order of limits; if we try to set \eta \rightarrow 0 first, the time dependence vanishes and we just get W_{fi} = 0. If we take the t limit first, it seems to diverge. But we can apply l’Hopital’s rule under the time limit to get \lim_{t \rightarrow \infty} \frac{e^{2\eta t}}{t} = \lim_{t \rightarrow \infty} 2\eta e^{2\eta t}. With this replacement, now we can take the \eta limit, but things are still delicate. We now have W_{fi} = \lim_{t \rightarrow \infty} \lim_{\eta \rightarrow 0} \frac{\eta}{\omega_{fi}^2 + \eta^2} \frac{2 |V_{fi}|^2}{\hbar^2} e^{2\eta t}. The first term is zero unless \omega_{fi} = 0, in which case it is infinite. This should remind you of a delta function, and in fact if we use the integral definition \delta(x-a) = \frac{1}{2\pi} \int_{-\infty}^\infty dk e^{ik(x-a)}, it’s straightforward to show that \lim_{\eta \rightarrow 0} \frac{\eta}{\omega_{fi}^2 + \eta^2} = \frac{1}{2} \lim_{\eta \rightarrow 0} \int_{-\infty}^\infty dk e^{ik\omega_{fi}-\eta|k|} = \pi \delta(\omega_{fi}).
Taking this limit, the remaining time-dependence goes away and we recover the familiar result for the golden rule, absorbing one factor of \hbar back into the delta function: W_{fi} = \frac{2\pi}{\hbar} |\bra{f} \hat{V} \ket{i}|^2 \delta(E_f - E_i).
32.4.2 Second-order transition amplitude
Now let’s go back to the case for the amplitude to remain in the initial state. In this case, to see the physics we’re interested in, we will need to work to second order in perturbation theory. We’ll continue to compute interaction-picture transition amplitudes, so the expression we have is: U_{ii}^{(I)} = 1 -\frac{i}{\hbar} V_{ii} \int_{t_i}^t dt' e^{\eta t'} + \left( -\frac{i}{\hbar} \right)^2 \int_{t_i}^t dt_1 \int_{t_i}^{t_1} dt_2 e^{\eta(t_1 + t_2)} \sum_n |\bra{n} \hat{V} \ket{i}|^2 e^{-i\omega_{ni} t_1} e^{i\omega_{ni} t_2}. In the first integral, the energy-dependent phases cancel with the same initial and final state, and so the first-order term evaluates to simply (with t_i \rightarrow -\infty) U_{ii}^{(I,1)} = -\frac{i}{\hbar} \frac{V_{ii}}{\eta} e^{\eta t}. For the second order term, it will take a bit more work. Doing the t_2 integral first, we have \frac{-1}{\hbar^2} \sum_n |V_{ni}|^2 \frac{1}{i\omega_{ni} + \eta} \int_{t_i}^{t} dt_1 e^{-i\omega_{ni} t_1} e^{(\eta + i\omega_{ni})t_1} e^{\eta t_1} \\ = -\frac{1}{2\hbar^2} \sum_n \frac{|V_{ni}|^2 / \eta }{i \omega_{ni} + \eta} e^{2\eta t}, with the frequency factors cancelling out in the dt_1 integral.
Now, at this point we can recombine things, square to get a probability, and then take the limit \eta \rightarrow 0. If we do so, we find some cancellation leads to a very simple result for the probability, through second order: p_{i \rightarrow i}(t) = 1 - \frac{1}{\hbar^2} \sum_{n \neq i} \frac{|V_{ni}|^2}{\omega_{ni}^2 + \eta^2} e^{2\eta t} = 1 - \sum_{n \neq i} p_{i \rightarrow n}(t). This is just the expected simple relation from conservation of probability, so it’s a good check on our setup so far. However, to see the interesting physics we’re looking for, we need to look more closely at what happens to the amplitude itself when we take our limits.
We would like to take the limit t \rightarrow \infty and see something constant happening, since we are applying a constant perturbation (as \eta \rightarrow 0.) However, we can’t just define a rate in the same way as for transitions to different states; a rate for something not happening doesn’t really make sense at face value. Instead, let’s adopt the ansatz that the amplitude evolves in time as a simple exponential, obeying the equation i\hbar \frac{dU_{ii}}{dt} = \Delta_i U_{ii}, with d\Delta_i/dt = 0, so that U_{ii}(t) = e^{-i\Delta_i t/\hbar}. If this equation is true, then we can compute the constant directly from our formula for the transition amplitude. First, let’s write out the full amplitude again and simplify a bit: U_{ii}^{(I)}(t) = 1 - \frac{i}{\hbar \eta} V_{ii} e^{\eta t} -\frac{1}{2\hbar^2} \frac{|V_{ii}|^2}{\eta^2} e^{2\eta t} - \frac{1}{2\hbar^2 \eta} \sum_{n \neq i} \frac{|V_{ni}|^2}{i\omega_{ni}^2 + \eta} e^{2\eta t}, splitting out the same-state term n=i from the sum. Proceeding with the ansatz, we see that
\Delta_i = i\hbar \frac{dU_{ii}/dt}{U_{ii}} \\ = i\hbar \frac{-\frac{i}{\hbar} V_{ii} e^{\eta t} - \frac{1}{\hbar^2 \eta} |V_{ii}|^2 e^{2\eta t} - \frac{1}{\hbar^2} \sum_{n \neq i} \frac{|V_{ni}|^2}{i\omega_{ni} + \eta} e^{2\eta t} + ...}{1 - \frac{i}{\hbar \eta} V_{ii} e^{\eta t} + ...} where we only need the first term in the denominator because we should work at consistent order in perturbation theory, meaning we should series expand the denominator and only keep terms up to order V^2. Doing so, we find \Delta_i = V_{ii} e^{\eta t} + \frac{i}{\hbar \eta} V_{ii}^2 e^{2\eta t} - \frac{i}{\hbar \eta} |V_{ii}|^2 e^{2\eta t} - \frac{i}{\hbar} \sum_{n \neq i} \frac{|V_{ni}|^2}{i \omega_{ni} + \eta} e^{2\eta t} + ... This will be constant once we take \eta \rightarrow 0, so the ansatz appears to have worked! The middle two terms cancel, but the last term is a bit delicate: so far, then, we have \Delta_i = \bra{i} \hat{V} \ket{i} + \lim_{\eta \rightarrow 0} \sum_{n \neq i} \frac{|\bra{n} \hat{V} \ket{i}|^2}{E_n - E_i + i \hbar \eta} e^{2\eta t}. Before we continue to simplify, we should notice that if we work at first order in perturbation theory, our result simply gives us a pure phase, which we recognize as the first-order energy correction in time-independent perturbation theory! In fact, if we go back from interaction picture to Schrödinger picture for the amplitude, we have U_{ii}(t) = \exp \left( -i (E_i + \Delta_i) t/\hbar \right), so we recognize that this is indeed just the same energy correction we found before.
32.4.3 Decay and natural width
Now let’s consider the second term; it looks similar to the second-order time-independent correction, but the limit we still need to take is delicate. At first glance, it may seem like we can simply set \eta = 0 and recover the second-order time-independent energy correction. If our Hilbert space is both finite and non-degenerate, then this is true and we’re done: \Delta_{i}^{(\rm finite)} = \bra{i} \hat{V} \ket{i} + \sum_{n \neq i} \frac{|\bra{n} \hat{V} \ket{i}|^2}{E_n - E_i}. However, this also means the dynamics is trivial: we find p_{ii}(t) = |U_{ii}(t)|^2 = 1, so our system remains permanently in state \ket{i}, just evolving by a phase. This is exactly what we should expect from the golden rule, since an adiabatic perturbation requires energy conservation, and we’ve specified that all of the other states have different energies.
If the Hilbert space is finite and some of the other states are degenerate, then things still aren’t very interesting: we know how to deal with that already, by diagonalizing \hat{H}_0 + \hat{V} over the degenerate subspace, so that the would-be divergent terms have zero matrix elements.
The only case which will lead to something interesting is the case where there are an infinite number of degenerate states, in which case we should replace our sum with an integration over the density of states: \sum_{n \neq i} (...) \rightarrow \int_0^\infty dE_n \rho_f(E_n) \frac{|V_{ni}|^2}{E_n - E_i + i\hbar \eta} e^{2\eta t}. Now the limit \eta \rightarrow 0 is delicate again, since it is regulating the divergence which occurs when E_n = E_i. Taking the limit requires some use of complex analysis; I’ll rely on the derivation in appendix A of Merzbacher and just skip to the resulting limit identity, which is only valid under an integral: \lim_{\epsilon \rightarrow 0^+} \frac{1}{x+i\epsilon} = \mathcal{P} \frac{1}{x} + i\pi \delta(x), where \mathcal{P} means “evaluate the Cauchy principal value of the integral with the function set to 1/x”. Since everything else in the integral is real, we can read off the real and imaginary parts of the correction term: {\rm Re}(\Delta_i^{(2)}) = \mathcal{P} \int_0^\infty dE_n \frac{\rho_f(E_n) |V_{ni}|^2}{E_n - E_i}, \\ {\rm Im}(\Delta_i^{(2)}) = \pi \int_0^\infty dE_n \rho_f(E_n) |V_{ni}|^2 \delta(E_n - E_i) or restoring the sum, {\rm Im}(\Delta_i^{(2)}) = \frac{\hbar}{2} \sum_{n \neq i} W_{i \rightarrow n}. We won’t go into the details of calculating these expressions in detail, but the key physical fact that we have obtained is that at second order, in systems where continuous decay channels are available from the state \ket{i}, the time evolution is now of the form \ket{i(t)} = U_{ii}(t) \ket{i} = \exp \left( -\frac{i}{\hbar} E_i t - \frac{\Gamma t}{2\hbar} \right) \ket{i}, so that now, p_{ii}(t) = |U_{ii}(t)|^2 = e^{-t / \tau}, with the lifetime set by the rates into other states, \frac{1}{\tau} = \sum_{n} W_{ni}. In other words, we have now effectively picked up an imaginary correction to the energy, which has led to a decay lifetime for the state \ket{i}. Ordinarily, we would think of an imaginary energy as something which violates unitarity; if we just consider the \ket{i} state alone, then it is a violation of unitarity, because our particle can “disappear” by transitioning into another state. If we keep track of the entire system, then of course unitarity is still satisfied and there are not really any imaginary energies present.
To make it apparent what the interpretation of the corrected energy means, it’s helpful to consider what the transition amplitude looks like in the energy domain instead of the time domain. We can do so by integrating: f(E) = \int dt\ e^{iEt/\hbar} e^{-\Gamma t/(2\hbar)} = \frac{1}{E - i\Gamma/2}. Squaring this, |f(E)|^2 = \frac{1}{E^2 + \Gamma^2/4}. For “sharp” energy levels, the time-domain evolution is as a pure phase e^{iEt}, which results in a delta function \delta(E) in the energy domain. Here, the presence of the decay has “broadened” the delta function, leading to a non-zero width in the energy domain. The width \Gamma is related to the lifetime \tau of the state as \Gamma = \hbar/\tau, so we can see another manifestation of energy-time uncertainty here: \Delta E = \hbar / \tau \Rightarrow (\Delta E) \tau = \hbar.
The inverse lifetime \Gamma can be observed in practice, and represents a fundamental limit on the precision with which we can measure the energy E of an unstable state, known as the natural width. There are other effects that contribute to natural width in practice, related to the fact that we don’t just see them in situations with adiabatic potentials, but more realistically with photons and radiation involved. But the story gets much more complicated, and we have now seen the basic phenomenon at work, so we’ll stop the discussion here.